Matlab incluye facilidades gráficas que permiten representar los datos y las operaciones de una manera cómoda para su interpretación. En este apartado veremos algunas de tales facilidades.

En primer lugar creemos una sinusoide y mostremos dicha sinusoide por pantalla. Para ello comenzamos creando un vector de abscisas, concretamente, un vector de muestras temporales separadas diez milisegundos:

>> X=0:(1/100):1;

A continuación, sobre dichas muestras temporales, definamos los puntos de la sinusoide:

>>Y=cos(2*pi*5*X);

Con ello habremos creado muestras de una sinusoide de 5 Hz. Para comprobar los resultados podemos ejecutar

>> plot(X,Y)

y el resultado debería ser el que se indica a continuación

La función plot dibuja una nueva figura en la ventana activa (en todo momento Matlab tiene una ventana activa de entre todos las ventanas gráficas abiertas), o abre una nueva figura si no hay ninguna abierta, sustituyendo cualquier cosa que hubiera dibujada anteriormente en esa ventana. A continuación, puede probarse lo siguiente (se comienza cerrando la ventana activa, para que al crear la nueva ventana aparezca en primer plano):

>>% el carácter % se utiliza para añadir código que no se ejecuta (comentarios)

>> close % se cierra la ventana gráfica activa anterior

>> grid % se crea una ventana con una cuadrícula

>> plot(X,Y) % se dibuja la función coseno borrando la cuadrícula

El resultado en este caso es el mismo que el anterior. Se puede observar la diferencia con la secuencia que sigue:

>> close

>> plot(X,Y) % se crea una ventana y se dibuja la función coseno

>> grid % se añade la cuadrícula sin borrar la función coseno

Ahora debería obtener la siguiente figura:

En el primer caso MATLAB ha creado la cuadrícula en una ventana nueva y luego la ha borrado al ejecutar la función plot. En el segundo caso, primero ha dibujado la función y luego ha añadido la cuadrícula. Esto es así porque hay funciones como plot que por defecto crean una nueva figura, y otras funciones como grid que se aplican a la ventana activa modificándola, y sólo crean una ventana nueva cuando no existe ninguna ya creada. A continuación veremos cómo (mediante la función hold) pueden añadirse gráficos a una figura ya existente respetando su contenido.

Pruebe ahora lo siguiente: 

>>Z=cos(2*pi*2.5*X);

>>hold on

>>plot(X,Z)

Debería obtener la siguiente figura:

Con esta secuencia de comandos hemos dibujado en la misma gráfica otra sinusoide de frecuencia 2.5 Hz. En este momento resulta interesante explorar cómo se pueden dibujar las dos sinusoides mediante diferentes colores sin más que añadir un tercer argumento a la función plot. Ejecute help plot y podrá ver las distintas opciones que se le presentan.

Observemos ahora lo que ocurre si intentamos representar una sinusoide de mayor frecuencia. Ejecute lo siguiente:

>>close all; % cerramos todas las ventanas gráficas

>>W=cos(2*pi*20*X);

>>plot(X,W)

Obtendrá la siguiente figura:

El gráfico obtenido en este caso no se corresponde con la sinusoide esperada. Lo que ocurre es que Matlab representa los puntos que contiene el vector W frente a los del vector X y utiliza líneas por defecto para unirlos. Cuando el número de puntos es suficientemente grande, no apreciamos distorsión en la figura. Sin embargo, cuando no contamos con muestras suficientes, la representación obtenida no coincide con lo esperado. Para observar las muestras que realmente pinta Matlab (sin las líneas que las unen), basta con teclear lo siguiente:

>>plot(X,W,'o')

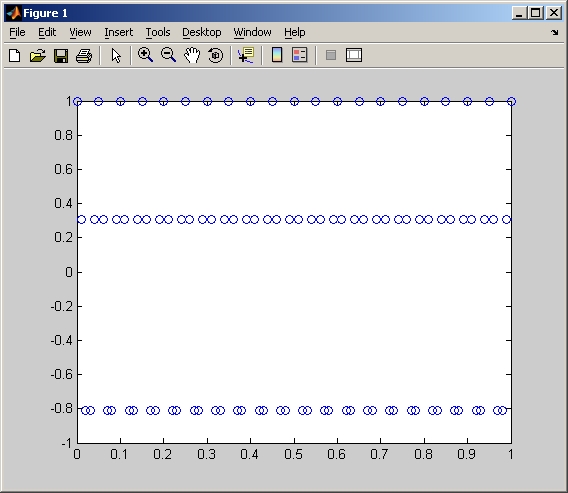
En este caso hemos utilizado el símbolo "o" para representar la función, evitando las líneas que automáticamente incluye Matlab. De nuevo consultando la ayuda en línea se puede investigar sobre ésta y otras posibilidades de la función plot. En concreto, resulta interesante ver qué ocurre cuando la función sólo recibe un vector como argumento, cuando alguno de los argumentos es una matriz, y otras posibilidades de representación conjunta sin hacer uso de la orden hold.

Para ver correctamente la sinusoide de 20 Hz, bastaría con utilizar un eje de abscisas más "granulado":

>>X2=0:(1/1000):0.2; %abscisas con menor separación (nótese que representamos sólo hasta 0.2)

>>W2=cos(2*pi*20*X2);

>>plot(X2,W2)

La figura obtenida en este caso es la que se muestra a continuación. Nótese que el número de períodos representados ha disminuido debido a que sólo se toman puntos hasta 0.2 en el eje de abscisas.

Otro tipo de representación es el conocido como diagrama de dispersión. En este caso se pretende mostrar cómo se distribuyen en el plano un determinado conjunto de datos obtenido. Cada dato vendrá definido por su par de coordenadas (x,y). Concretamente:

>> abscisas=randn(100,1);
>> ordenadas=abscisas+rand(100,1);
>> scatter(abscisas,ordenadas)

En este ejemplo se ha creado el vector  abscisas, consistente en 100 números aleatorios. A continuación se ha creado el vector ordenadas sumando a abscisas otro vector de números aleatorios independiente del anterior. Finalmente, se muestra en pantalla el diagrama de  dispersión correspondiente a estos datos así creados.  El resultado (en cada ejecución será distinto) tendrá un aspecto como el que mostramos a continuación

Ejercicio: haciendo uso de la orden polar, dibuje en pantalla una circunferencia de radio a escoger. Debería obtener algo parecido a la siguiente figura: