Noise modeling and estimation

maquina.jpg

Abstract

Noise is known to be one of the most common sources of deterioration of the quality of Magnetic Resonance Imaging (MRI) data. The principal source of noise in most MR scans is the subject or object to be imaged, followed by electronics noise during the acquisition of the signal in the receiver chain. It is produced by the stochastic motion of free electrons in the RF coil, which is a conductor, and by eddy current losses in the patient, which are inductively coupled to the RF coil. The presence of noisy patterns on the acquired MR signal is a problem that affects not only the visual quality of the images, but also may interfere with further processing techniques such as registration, fMRI analysis or tensor estimation in Diffusion Tensor MRI. The accurate modeling of signal and noise statistics in MR data usually underlies the tools for processing and interpretation within MRI.

The stationary Rician distribution has been widely accepted in literature as a suitable model for noise in MR magnitude images. Many authors have precisely introduced the Rician statistics in the estimation of diffusion models , curve fitting for quantitative perfusion measurements, hypothesis tests to assess the activation level in functional MRI, in a preprocessing step to remove the bias of the data for the subsequent processing stages and denoising techniques.

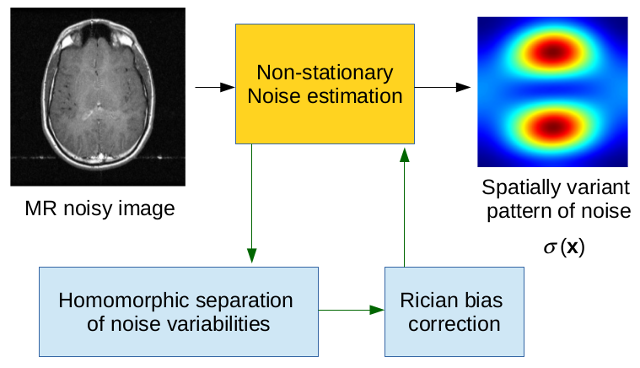
The main assumption for single coil Rician acquisitions is that the noise is stationary, and therefore a single value of sigma characterizes the whole data set. However, this premise will mostly fail when considering modern scanners with multiple-coil antennae and scanning software to correct artifacts, and to improve the final appearance of the image, which is the case for accelerated acquisitions with parallel MRI (pMRI) reconstruction techniques. If GRAPPA (Generalized Autocalibrating Partially Parallel Acquisition) is used for reconstruction, the final noise is known to follow a non-stationary nc-chi distribution, while if SENSE (Sensitivity Encoding for Fast MRI) is used, the magnitude signal may be considered Rician distributed with a spatially variant value of sigma.

paper_media_14.png

Books

Papers:

  • Santiago Aja-Fernández, Gonzalo Vegas-Sánchez-Ferrero, Antonio Tristán-Vega, Noise Estimation in Parallel MRI: GRAPPA and SENSE, Magnetic Resonance Imaging, Volume 32, Issue 3, April 2014, Pages 281–290 doi.
  • Santiago Aja-Fernández, Véronique Brion, Antonio Tristán-Vega, Effective Noise Estimation and Filtering from Correlated Multiple-Coil MR data, Magnetic Resonance Imaging, Volume 31, Issue 2, February 2013, Pages 272–285. doi.
  • S. Aja-Fernández, A. Tristán-Vega, Influence of Noise Correlation in Multiple-Coil Statistical Models with Sum of Squares Reconstruction. Magnetic Resonance in Medicine. Volume 67, Issue 2, pages 580–585, February 2012doi
  • S. Aja-Fernández, A. Tristán-Vega, S. Hoge. Statistical Noise Analysis in GRAPPA using a parametrized non-central chi approximation model. Magnetic Resonance in Medicine. Volume 65, Issue 4, pages 1195–1206, April 2011 doi
  • S. Aja-Fernández, G. Vegas-Sánchez-Ferrero, A. Tristán-Vega. About the background distribution in MR data: a local variance study. Magnetic Resonance Imaging Vol. 28, No. 5, Jun. 2010, pp 739-752. doi
  • S. Aja-Fernández, A. Tristán-Vega, C. Alberola-López, Noise estimation in single- and multiple-coil magnetic resonance data based on statistical models, Magnetic Resonance Imaging, Vol. 27, No. 10, Dec. 2009, pp. 1397-409. doi
  • S. Aja-Fernández, M. Martín-Fernández and C. Alberola-López, "Automatic Noise Estimation in Images Using Local Statistics. Additive and Multiplicative Cases. Image and Vision Computing, Vol. 27, Issue 6, May 2009, pp. 756-770. doi
  • S. Aja-Fernández, C. Alberola-Lopez and C.-F. Westin. "Noise and Signal Estimation in Magnitude MRI and Rician Distributed Images: A LMMSE Approach", IEEE Trans. on Image Processing, Vol. 17, No. 8, Aug. 2008, pp. 1383-1398. do

Software

  • Noise estimation techniques for MR data [Matlab Exchange][Matlab]: Main methods to estimate noise out of MR data from different authors. All methods are compared in

    S. Aja-Fernández, A. Tristán-Vega, C. Alberola-López, Noise estimation in single- and multiple-coil magnetic resonance data based on statistical models, Magnetic Resonance Imaging, Volume 27, Issue 10, Pages 1397-1409.

  • Simulator of noisy parallel acquisition MR data (GRAPPA and SENSE included) [Matlab Exchange][Matlab].
  • LMMSE filter for Rician MRI data [Slicer Module][Matlab][Matlab Exchange], as described in

    S Aja-Fernández, M. Niethammer, M. Kubicki, M. E. Shenton, C.F. Westin, "Restoration of DWI data using a Rician LMMSE estimator". IEEE Tr. on Medical Imag. Vol. 27, No. 10, Oct. 2008, pp. 1389-1403.

  • Efficient and Robust Nonlocal Means for MRI denoising [ITK][Slicer Module][Matlab], as defined in

    A. Tristán-Vega, V. García-Pérez, S. Aja-Fernández, Efficient and Robust Nonlocal Means Denoising of MR Data Based on Salient Features Matching, Computer Methods and Programs in Biomedicine. Volume 105, Issue 2, February 2012, Pages 131–144