4. PERDIDAS POR REFLEXIóN          Anterior   A índice   Siguiente

  

El calculo de las perdidas por reflexión es mas complicado que el de las perdidas por absorción.

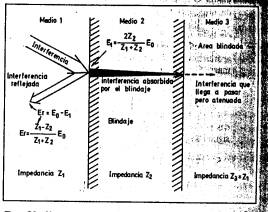
          Las perdidas por reflexión en la frontera entre dos medios (aire y blindaje o entre dos distintos metales) están relacionadas con las impedancias características de cada uno de los dos medios. Según se puede ver en la figura 8, una onda incidente es parcialmente reflejada en la superficie de un blindaje. El resto es transmitida a través del blindaje. Las ecuaciones dadas en las figuras pueden aplicarse también substituyendo E por H y en ellas no se ha contemplado la reflexión en la segunda cara.

          Cuando una onda atraviesa un blindaje, encuentra dos cambios de medio, y si este es delgado en comparación con la profundidad de penetración d, al tener pocas perdidas por absorción, habrá múltiples reflexiones. Si el blindaje es metálico (medio 2 en la figura 8) y el área que lo rodea es aire (medio 1),entonces Z1 es mucho mayor que Z2 y la mayor reflexión ocurre cuando la onda penetra en la pared exterior del blindaje en el caso de campos eléctricos y cuando la onda deja la cara interna del blindaje en el caso de campos magnéticos.


  Figura 8. Una onda incidente es parcialmente reflejada en la superficie de un blindaje. El resto es transmitida a través del blindaje. Las ecuaciones dadas pueden aplicarse también sustituyendo E por H. Aquí no se ha contemplado la reflexión en la segunda cara para una mayor claridad.

                                                                                                  Ir al principio

   La impedancia de cualquier material esta dada por:

                |Z| = E/H = 3,68·10-7·Öf·Ö(mr·sr)

donde f esta dada en Hz y las demás variables han sido definidas anteriormente. Para el aire o el vacio, esta impedancia vale 337 OHM.

En el caso de campos eléctricos, los blindajes delgados también son efectivos debido a la reflexión en la primera superficie. Sin embargo en el caso de campos magnéticos, al tener la reflexión principal en la segunda superficie, se tienen múltiples reflexiones y por ello la efectividad del blindaje queda reducida, como ya se ha visto en el apartado anterior. Las perdidas por reflexión aumentan al disminuir la frecuencia y aumentar la conductividad del material.

   


       Figura 9. Vectores E y H de una onda plana electromagnética en un cierto instante, estando E y H en fase, perpendiculares entre si y dirigiéndose hacia x.

                                                                                                          Ir al principio

     En el caso de campos electromagnéticos (ondas planas) (figura 9), la impedancia antes de penetrar en el blindaje es igual a la impedancia característica del vacio Z0 (377 OHM), y cuanto menor es la impedancia del material del blindaje, mayores son las perdidas por reflexión.

         En el campo cercano, la impedancia E/H depende de la fuente del campo (antena) y no del medio de propagación, al contrario de lo que ocurre en el campo lejano. Un campo eléctrico con alta impedancia tiene mayor reflexión que una onda plana, siendo las perdidas por reflexión el principal mecanismo de apantallado en el caso de campos eléctricos. Un campo magnético de baja impedancia tiene menor reflexión que un onda plana, debido a que las perdidas por reflexión son función del cociente entre la impedancia de onda y la impedancia de blindaje.

         Las ecuaciones para el calculo de las perdidas por reflexión para los tres casos anteriores, son las siguientes:

                       R = 141,7 – 10 log(mr f 3 d2/sr) dB

para campos eléctricos,

                       R = 74,6 – 10 log((mr f/sr) dB

para campos magnéticos,

                       R = 108,1 – 10 log(mr f/sr) dB

para campos electromagnéticos, estando la distancia “d” en cm y la frecuencia f en MHZ. Aquí igualmente se pueden extraer los datos para mr y sr de la tabla3.

                                                                                                          Ir al principio


          Figura 10. Pérdidas por reflexión en el caso de ondas planas para diversos materiales. Las perdidas son mayores a bajas frecuencias y para materiales de lata conductividad. Aquí, en el caso del hierro y el hypernick se supone que en la permeabilidad es constante con la frecuencia. Estas graficas son validas para espesores mayores a 3d, siendo  d la profundidad de penetración.

 

Las perdidas por reflexión en el caso de ondas planas (campo electromagnético lejano),se presentan en la figura 10 para diversos materiales. Las perdidas son mayores a bajas frecuencias y también son mayores en los materiales de alta conductividad. Aquí en el caso del hierro puro (hierro dulce)y el hypernick (ver datos de estos materiales en la tabla 3)se supone que la permeabilidad es constante con la frecuencia. Estas graficas son validas para espesores que tres veces la profundidad de penetración de cada material. Las perdidas totales para una onda plana son equivalentes a la suma de las perdidas de absorción A, mas las de reflexión R (figura 1).En este caso se desprecia el termino B relacionado con las reflexiones múltiples debido a que las perdidas de reflexión son suficientemente altas con ondas planas.                                                     Ir al principio

                                                                                                         


         Figura 11. Efectividad de un blindaje de cobre de 0,5 mm de espesor en el caso de un campo electromagnético lejano (ondas planas).

                                                                                                                                Ir al principio

                    Ir al principio
       Figura 12. (a) Pérdidas por reflexión R para campos eléctricos (campo cercano) para diversos materiales y varias distancias d desde el emisor.(b) Pérdidas por reflexión R para campos magnéticos (campo cercano) para diversos materiales y varias distancias d desde el emisor. En los dos casos se supone que la permeabilidad es constante con la frecuencia.


        Figura 13. Efectividad de un blindaje de cobre en función de la frecuencia para una distancia entre el emisor y el blindaje de 1 metro para varios espesores. Puede utilizarse también para otros materiales buenos conductores como: aluminio, latón, oro y plata con muy pocos decibelios de diferencia.

                                                                                                      Ir al principio

Con campos eléctricos, el principal mecanismo de apantallado a baja frecuencia es la reflexión, y a alta frecuencia, lo es la absorción. A bajas frecuencias es difícil apantallar eficientemente contra campos magnéticos porque su efectividad es baja.

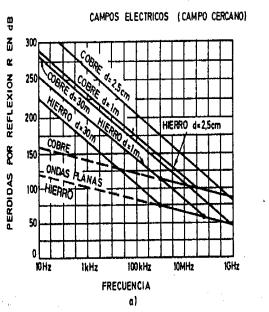
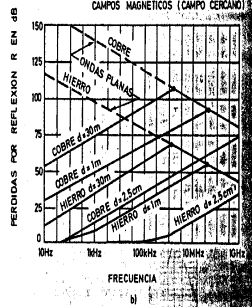
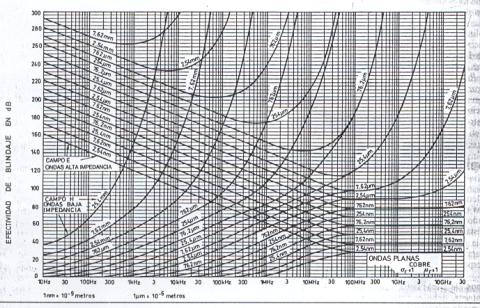
         La figura 12 muestra las perdidas por reflexión de varios materiales en el caso de campos eléctricos y campos magnéticos. La figura 13 muestra el gráfico de la eficiencia de un blindaje de cobre en función de la frecuencia para una distancia entre el emisor y el blindaje de 1 metro para varios espesores.


       Figura 14. Efectividad de un blindaje típico de alta permeabilidad en función de la frecuencia para una distancia entre el emisor y el blindaje de 1 metro para varios espesores.

                                                                                                                                                                                                                       Ir al principio

 

Puede utilizarse también para otros materiales buenos conductores como aluminio, latón, oro y plata con muy pocos decibelios de diferencia.

         La figura 14 presenta la efectividad de un blindaje de alta permeabilidad en función de la frecuencia para una distancia entre el emisor y el blindaje de 1 metro para varios espesores. Las dos últimas figuras incluyen las perdidas de absorción A y reflexión R. Por último, a modo de resumen esquemático, la figura 15 plantea la metodología del calculo de un blindaje de forma sistemática, utilizando las ecuaciones explicadas anteriormente.