Aproximación científica a los sonidos musicales
Asignatura: Ingeniería de la Ondas I
E. T. S. de Ingenieros de Telecomunicación
Universidad de Valladolid (España)
José Luis Gutiérrez Sacristán -
jgutsac@ribera.tel.uva.es
Introducción:
El objetivo del presente trabajo es realizar un estudio
científico de los sonidos producidos por los instrumento musicales: su
naturaleza física y la sensación auditiva que producen. Las cualidades
distintivas de estos sonidos musicales irán revelándose según vayamos
tratando diferentes aspectos físicos y perceptivos. Un enfoque clásico y
restrictivo de cuáles sonidos pueden ser considerados musicales es razonable y
surge naturalmente de las facultades perceptivas del oído humano, como
veremos.
Como estamos tratando un última instancia con una sensación,
resultará insuficiente estudiar sólo las propiedades de la onda de presión
sonora incidente en el tímpano, pues a lo largo de todo el sistema auditivo se
producen diferentes procesos de acondicionamiento y transformación de la
señal, determinantes de las capacidades y limitaciones perceptivas del sistema
auditivo humano.
La trasformación de mayor gravedad se lleva a cabo en el oído
interno, donde una señal mecánica se transforma en impulsos nerviosos: La onda
mecánica entrante en la cóclea (sólo adaptada su impedancia respecto la del
tímpano) es una señal "analógica", toma valores de un continuo, mientras que
por la naturaleza neuronal, la señal que viaja por una fibra nerviosa es de
tipo "digital", es decir, un tren de pulsos. Partiendo de la cóclea, Por el
nervio auditivo viajan aproximadamente 24.000 fibras nerviosas
[1] capaces cada una de
ellas portar una señal de este tipo.
Enlazando con las propiedades de los sonidos musicales, como
consecuencia directa de las procedimientos neuronales de decodificación de las
señales nerviosas auditivas en el cerebro, nuestro oído está muy especialmente
adaptado para el análisis de un tipo restringido de señales: aquellas
que como las producidas en cavidades u otros sistemas de resonancia (por
ejemplo, un tubo de un órgano, la laringe humana o una cuerda de un
violín) irradian a través del aire su energía muy concentrada en torno de sus
frecuencias de resonancia.
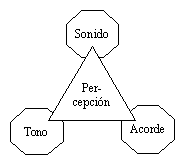
Los sonidos musicales tienen unas propiedades especiales en
términos perceptivos. Según Erickson [2], pueden situarse en diferentes puntos
de un triángulo según la forma en que los escuchemos:
 |
-
El tono corresponde a la propiedad del sonido de
ser ordenado en una escala, análoga a una ordenación en frecuencias, pero desde
el punto de vista de la sensación.
-
Acorde se refiera la la propiedad de diferenciar en
un sonido varias componentes con diferentes tonos.
-
Sonido la cualidad asociada a un análisis no
realizado en términos de tono ni acorde.
|
Vislumbrada la variedad de fenómenos interrelacionados
alrededor del sonido musical acometeremos el estudio desde los siguientes puntos de vista:
-
Acústica fisiológica: los fenómenos acaecidos
sobre la vibración sonora desde que excita el tímpano hasta que se convierte
en señales neuronales que viajan camino del cerebro por el nervio auditivo.
-
Psicoacústica: la sensación sonora
(percepción) sometida a
análisis y experimentación.
-
Acústica física: la base física de la
generación de sonidos en los instrumentos musicales.
-
Teoría matemática de la comunicación:
necesaria para construir herramientas de análisis de la señal sonora y de
los sistemas que la acondicionan y distorsionan en el sistema auditivo.
-
Teoría de la música / Armonía: qué
relaciones establecen los músicos entre los sonidos generados por los
instrumentos musicales.
Diagrama esquemático del estudio:

Índice:
1.- Acústica fisiológica
 En este apartado vamos a seguir el camino y transformaciones de la señal
auditiva desde que incide en el tímpano hasta que recorre el nervio auditivo
camino del cerebro.
En este apartado vamos a seguir el camino y transformaciones de la señal
auditiva desde que incide en el tímpano hasta que recorre el nervio auditivo
camino del cerebro.
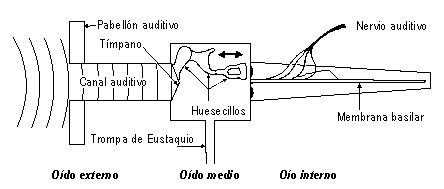
La onda de presión sonora que viaja por el aire incide en el pabellón
auditivo y viaja por el oído externo (responsable de resonancias
perceptibles en la sensibilidad del oído) hasta incidir en el tímpano
El tímpano es la fina membrana que separa el oído externo del oído
medio, donde se alojan los huesecillos. Por una parte actúa como transductor de
la vibración que le transmite la onda de presión sonora incidente desde el
exterior, al mismo tiempo que impide que cualquier partícula penetre en el oído
medio. El oído medio está herméticamente cerrado del exterior, excepto por la
trompa de Eustaquio, comunicada con la garganta, que se abre durante breves
lapsos de tiempo para compensar excesos o defectos de presión y servir como
conducto de drenaje.
En el oído medio, los huesecillos (martillo, yunque y estribo), actúan
como un sistema de palancas, comunicando la onda mecánica desde el tímpano
(sobre el que se apoya el martillo) hasta la cóclea, por de la ventana oval
(sobre la cual se apoya el estribo). Realizan una importante labore de
adaptación de impedancias que permite que la presión que ejerce el estribo
en la membrana oval sea 30 veces mayor que la ejercida sobre el tímpano.
En todo momento hasta ahora, la señal que se ha transmitido mecánicamente
hasta la ventana oval de la cóclea es una señal análoga a la señal de
presión sonora que viajaba por el aire procedente de la fuente de sonido.
La ventana oval supone el punto de entrada de esta señal en el
oído
interno. El único órgano responsable de la audición en el oído interno es la
cóclea, donde se llevará a cabo la conversión de la señal analógica que hemos
mencionado en miles de señales nerviosas que viajarán por el nervio auditivo
hacia el cerebro. Estas señales, que por la naturaleza neuronal son de tipo
digital (trenes de pulsos), tienen que transmitir toda la información de
interés en la señal original, y además codificada adecuadamente para que el
cerebro pueda interpretarla.
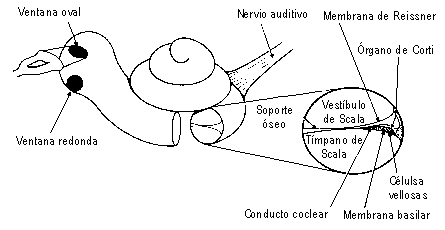
La cóclea es una estructura con forma de tubo cónico alargado, que se
encuentra enrollada sobre sobre sí misma en forma de espiral. Observando una
sección transversal se aprecian tres diferentes cámaras que la recorren en toda
su longitud: el dos canales y el conducto coclear. La cóclea está llena de
líquido y rodeada por paredes óseas rígidas. Hay diferentes líquidos en los
canales que en el conducto coclear, que se encuentran separados por dos
membranas. La membrana de Reissner [ver ilustración] es extraordinariamente
delgada. Apoyados en la membrana basilar se encuentra el complejo y delicado
órgano de Corti, que contiene varias filas de diminutas células vellosas a las
cuales se conectan las fibras nerviosas. Cada fila de células vellosas contiene
unas 7000 células, habiendo un total de 24.000 células en varias filas. Cada
célula vellosa posee numerosos cilios, que se doblan cuando la membrana basilar
responde a un sonido, desencadenando una señal nerviosa en el nervio auditivo.
Georg von Békésy recibió el premio
Nóbel de Fisiología y Medicina en 1961 por su descubrimiento del funcionamiento
de la cóclea y su membrana basilar. Realizó numerosos experimentos con cócleas
de animales y cadáveres, y construyo modelos que imitaban su funcionamiento con
el objetivo de desentrañar el patrón de vibración de la membrana basilar ante
las diferentes frecuencias y amplitudes de las señales entrantes. Encontró
indicios de realimentación en las características mecánicas de la cóclea que
hacían que las extraídas de animales perdiesen selectividad en frecuencia al
cabo de pocos minutos de la muerte del animal.
Para comprender cómo vibra la membrana basilar imaginamos la cóclea
desenrollada, con forma de cilindro estrecho dividido en dos secciones por la
membrana basilar. En primera aproximación no es necesario considerar el conducto
coclear por lo extremadamente fino que es. En el extremo más grande del cilindro
se encuentran las ventanas oval y redonda, cada una de ellas cerrada por una
membrana. En el otro extremo de la membrana basilar hay un pequeño orificio
denominado helicotrema que comunica las dos secciones. La membrana basilar acaba
a poca distancia del extremo del cilindro, con lo cual el fluido puede
transmitir ondas de presión de vuelta desde el final de la membrana.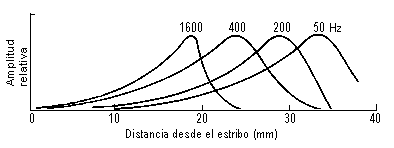
Cuando el estribo vibra contra la ventana
oval, se producen oscilaciones en la membrana basilar según la vibración viaja a
través del interior de la cóclea. Los tonos agudos hacen vibrar la membrana
basilar cerca de las ventanas (donde es delgada y rígida), mientras que los
tonos graves hacen vibrar la membrana basilar cerca del helicotrema, donde es
más flácida.
De este modo, en la cóclea tiene lugar un análisis espectral inicial. La
conversión de las vibraciones mecánicas de la membrana basilar en impulsos
eléctricos del nervio auditivo se lleva a cabo en el ya mencionado órgano de
Corti. En función de la frecuencia de la señal, la vibración se encontrará
localizada a lo largo de la membrana basilar excitando unas u otras fibras
nerviosas (correspondientes a las diferentes frecuencias). Asimismo, en función
de la amplitud de la vibración, más fibras nerviosas serán estimuladas.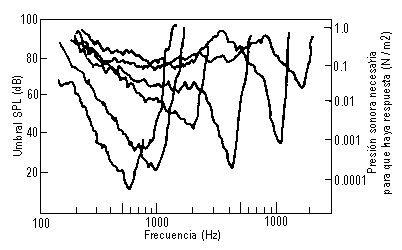
Hermann von Helmholtz (1821-1894) identificó que el patrón de vibración en el
interior de la cóclea hacía que la respuesta de cada fibra nerviosa
correspondiese a la de un resonador selectivo sintonizado a diferentes
frecuencias en función de la posición que ocupase cada terminación nerviosa a lo
largo de la membrana basilar. Es lo que se conoce como teoría del lugar.
Los experimentos posteriores de Georg von
Békésy demostraron que esta aproximación es cierta, pero que las bandas de
filtrado no son lo suficientemente estrechas como para justificar la precisa
percepción del tono del oído humano, aunque, como veremos en el siguiente
apartado, sí son de vital importancia para
permitir que cada fibra nerviosa se capaz de transmitir correctamente una señal,
restringiendo su actuación a una banda de frecuencias, que denominaremos
banda crítica.
[Volver al índice]
2.- Psicoacústica
Como hemos mencionado anteriormente, una célula nerviosa es excitada cuando
la vibración de la membrana basilar supera un cierto umbral. Existen células con
diferentes umbrales para permitir un gran rango dinámico de respuesta al oído.
Asimismo, la señal que viaja por cada fibra nerviosa individual del nervio
auditivo, aún tratándose de un tren de pulsos, posee la misma periodicidad que
la envolvente temporal de la señal filtrada en banda correspondiente a la
vibración de la membrana basilar allí donde esta su terminación nerviosa.
La teoría de la periodicidad
afirma que el cerebro es capaz de decodificar los patrones temporales de cada
fibra nerviosa, analizando la autocorrelación dentro de cada señal individual,
así como correlación cruzada entre fibras correspondientes a distintas bandas
críticas buscando patrones temporales de vibración cuya periodicidad está
relacionada por números enteros. Según esta teoría, es deseable que cada fibra
individualmente reciba sólo una señal armónica, pues si el patrón de vibración
de cada fibra nerviosa fuese demasiado complicado, conteniendo componentes de
diferentes periodicidades, las búsqueda de correlación no podría acometerse. Así
surge la necesidad de filtrado en banda (bandas críticas) previo de cada señal
nerviosa que se lleva a cabo en la cóclea como hemos visto en el apartado
anterior.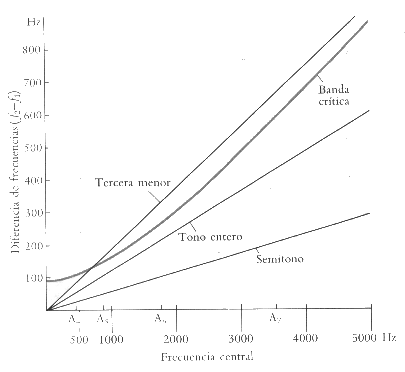
Llamamos Banda crítica a la banda de frecuencias que excita cada
terminación nerviosa. Mediante estudios fisiológicos de cócleas, así como
experimentos perceptivos sabemos que el ancho de banda de estos filtros
pasabanda centrados en cada terminación nerviosa es tal que se abarcaría la
totalidad del espectro audible con 24 de ellos. Pero no debemos olvidar que no
existen 24 filtros, sino un continuo, pues el filtrado es el resultado de las
propiedades de mecánicas de la cóclea sobre cada punto de la membrana basilar.
El ancho de banda crítica es función de la frecuencia, como se observa en el
gráfico (en frecuencias, aproximadamente, un intervalo de tercera menor
corresponde a 1/5, un tono entero a 1/8, y un semitono a 1/16 de la frecuencia
central).
La percepción del tono
A mediados del siglo XVIII, A. Seebeck realizó una
serie de experimentos sobre la percepción del tono que produjeron sorprendentes
resultados. Como fuente de sonido, Seebeck utilizó una sirena consistente en un
disco rotatorio con orificios periódicamente espaciados por los que atravesaba
una ráfaga de aire. Cuando los orificios estaba regularmente distribuidos (a),
la sirena producía un sonido con un tono muy bien definido, correspondiente al
periodo entre ráfagas. Duplicando el número de orificios (b) el tono se elevaba
exactamente una octava. Sin embargo, utilizando un disco con orificios
espaciados distancias t1 y t2 (c) se produjo un resultado inesperado: el tono
percibido era el mismo que en el caso (a), aunque cambia el timbre, la calidad
del sonido.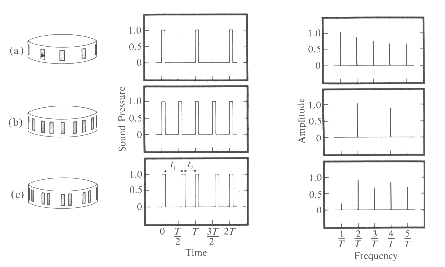
Casi simultáneamente, G. S. Ohm adaptó el teorema de análisis espectral de
Fourier a la acústica, formulando una hipótesis (ley de la acústica de Ohm,
también llamada 2ª ley de Ohm) según la cual sólo podía percibirse el tono
correspondiente a una determina frecuencia si la onda acústica tenía potencia en
dicha frecuencia. Ohm fue muy crítico con la interpretación de Seebeck según la
cual es la periodicidad no la potencia en la frecuencia fundamental lo que
determina el tono.
En el siglo XIX, H. von Helmholtz apoyaba la idea de Ohm, añadiendo
importancia a la llamada distorsión armónica, que generaría una fuerte
fundamental a partir de los armónicos superiores (tonos de suma y diferencia).
Sin embargo, es fácil construir un experimento para refutar el punto de vista de
Helmholtz: tomamos un sonido con fuertes armónicos parciales en frecuencias
múltiplos de una fundamental. Entonces filtramos la fundamental y añadimos un
armónico en una posición ligeramente desplazada respecto a la posición de la
fundamental original. Si el oído generase una fuerte fundamental a partir de los
armónicos superiores deberían percibirse batidos entre el armónico añadido y la
fundamental generada por el oído, lo cual no sucede.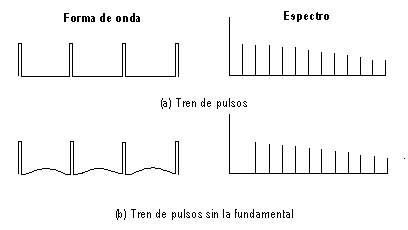
De hecho, no es necesario que una señal tenga nada de potencia en su
frecuencia fundamental, para que tenga una periodicidad de valor inverso a su
periodo. En la figura se observa un tren de pulsos al cual hemos restado su
armónico fundamental.
Es sencillo construir experimentos desplazando todas las componentes
armónicas de un sonido, donde se observa que la periodicidad de incluso la
envolvente de una onda es la que nos determina la percepción del tono.
En resumen, la percepción del tono en última instancia es realizada por el
cerebro en base a patrones de correlación temporal de las señales de las fibras
nerviosas. Sin embargo, no sería posible para el cerebro desentramar esta
información si no fuese porque diferentes fibras adquieren la periodicidad de
armónicos de diferentes frecuencias, los que recaen dentro de su correspondiente
banda crítica.
Tono virtual
Cuando un sonido está compuesto por parciales de frecuencias múltiplos de una
fundamental resulta fácil predecir que tono será percibido, pero cuando un
sonido está compuesto por parciales no armónicos, surge un problema. En este
tipo de sonidos no es sencillo encontrar una envolvente periódica y definida del
sonido. Actualmente se cree que el cerebro extrae una pequeña serie de armónicos
del centro de la banda audible, y determina el tono como el máximo común divisor
de la serie. En algunos instrumentos de percusión, como algunas campanas, existe
un parcial en la misma frecuencia que estima el cerebro a partir de los otros
parciales, reforzando la percepción del tono, mientras que en otros
instrumentos, como el gong, la percepción es puramente subjetiva.
Percepción absoluta del tono: Existe un interesante fenómeno relativo a la percepción del tono por el oído
humano. La inmensa mayoría de la gente es capaz de diferenciar si un sonido
es más agudo que otro, incluso, gente con una preparación previa es capaz de
distinguir el intervalo que separa dos sonido presentados uno a continuación
que otro con gran precisión. Sin embargo, existe un conjunto de personas
(0.01% de la población) que poseen la extraordinaria capacidad de
identificar el tono de un sonido sin que se les presente ningún tono de
referencia. Es lo que denominamos percepción absoluta del tono. Estas
personas pueden discriminar los sonidos como la mayoría de las personas los
colores.
Cómo estimar el grado de
consonancia/disonancia de un sonido
Para Helmholtz, el cerebro realiza un análisis espectral de la señal sonora,
separando un sonido en sus diferentes armónicos parciales. Experimentando
llegó a la
conclusión de que hay disonancia cuando la diferencia de
frecuencia entre dos parciales (tonos puros que componen el sonido musical)
es tal que se aparecen entre 30 y 40 batidos por segundo.
Investigaciones actuales [3] han llevado a la misma conclusión: la
consonancia o disonancia de dos tonos puros (los diferentes armónicos que
componen los sonidos musicales) que suenan juntos depende de la diferencia
de frecuencias, y no de su cociente. La máxima disonancia se produce cuando
la diferencia de frecuencias es aproximadamente ¼ del ancho de banda
crítico. También depende ligeramente del nivel de presión sonora. Como el
ancho de banda crítico depende de la frecuencia central de la banda,
disponemos de una fórmula empírica para calcular la diferencia de
frecuencias a la que se obtiene la mayor disonancia.: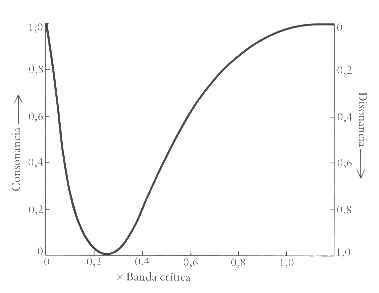
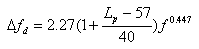
Siendo Lp el nivel de presión sonora y f la frecuencia del tono primario.
Puede elaborarse un algoritmo que calcule el grado de disonancia de un
sonido: Primero se normaliza el espectro del sonido a ancho de banda crítico
constante (normalizar a la fórmula anterior para Lp constante), y entonces se
convoluciona el espectro normalizado por la función que representa el grado de
disonancia que aparece según nos aproximamos a la banda crítica [ver gráfico].
La función obtenida representará la disonancia aparecida en función de la
frecuencia.
La explicación de este fenómeno en términos neurológicos se basa en el hecho
de que cuando dentro de la banda crítica correspondiente a una fibra nerviosa
recae sólo una componente armónica, la señal neuronal posee una perfecta
periodicidad que facilita al cerebro la búsqueda de correlaciones temporales.
Sin embargo, si dentro de la banda crítica recaen diferentes componentes
armónicas, la señal neuronal no posee una correlación fácil de desentrañar, lo
que provoca el stress o "tormento tormento perpetuo", tomando palabras de
Galileo, propio de una disonancia.
Efecto de no linealidades
Es difícil encontrar un sistema con una respuesta puramente lineal. Para
Helmholtz, la respuesta del oído no era lineal, de modo que el oído fortalecía o
reconstruía el armónico fundamental de un sonido a partir de sus armónicos
superiores. Como hemos visto en párrafos anteriores, el oído tiene una respuesta
muy lineal, de modo que no se lleva a cabo el fenómeno descrito por Helmholtz
con suficiente intensidad. Sin embargo sí que aparecen otros fenómenos más
tenues, pero importantes.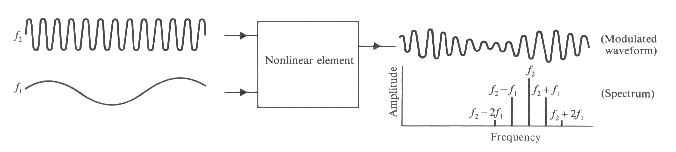
La distorsión interarmónica es uno de los fenómenos más importantes:
¿Cómo afecta la presencia de un armónico en el resto de armónicos?. Podemos
analizar la respuesta de un sistema mediante su desarrollo en serie de Taylor.
Resulta muy sencillo de estudiar el caso de un sistema con una componente
cuadrática en su respuesta, al que introducimos dos funciones armónicas.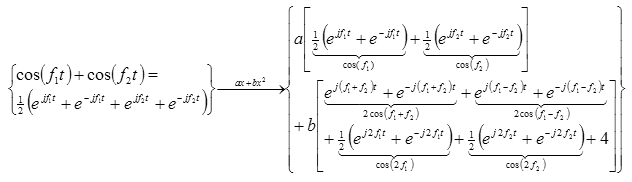
Como se puede observar en la fórmula anterior y escuchar en el
ejemplo sonoro, el oído genera
términos de diferencia así como armónicos superiores que antes no existían
(es la prueba de que el oído no es un sistema lineal).
Predominan los tonos de diferencia cuadráticos [ver fórmula]
y cúbicos, debido a los término de orden 2 y 3 en el desarrollo de Taylor de la
respuesta del oído.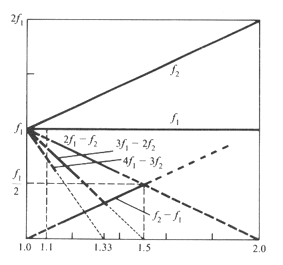
Los tonos de diferencia también son responsables de la aparición de muy
tenues batidos cuando se escuchan intervalos de quinta (3/2) y octava (2/1)
ligeramente desafinados. Algunos compositores como E. Varese, han aprovechado
los tonos de diferencia para construir melodías que suenan en registros mas
graves que los que pueden alcanzar los intérpretes.
[Volver al índice]
3.- Acústica
física
Los instrumentos musicales se caracterizan por estar construidos con el
propósito de producir un sonido con unas características adecuadas para la
música. Podemos distinguir los instrumentos en tres grupos, en función de las
características del sonidos que producen:
- Sonido de tono bien definido y apto para construir armonía musical
- Instrumentos de cuerda y viento
- Sonido de tono aceptablemente definido, pero no aptos para la armonía
convencional
- Algunos instrumentos de percusión como xilófono, marimba, carillón, celesta,
campanas tubulares y timbales
- Sonidos sin tono definido, limitados para ritmos o sonidos de timbre "exótico"
distinto de los anteriores.
- El resto de instrumentos de percusión: gong, bombo, platillos...
Instrumentos que producen un sonido de tono
bien definido y apto para construir armonía musical
Los instrumentos de cuerda y viento se caracterizan por poseer una estructura
que vibra en frecuencias son múltiplos enteros de una fundamental, transmitiendo
al aire un sonido compuesto por parciales así relacionados (por parcial
entendemos una oscilación de tipo armónico centrada en una frecuencia
particular).
En primera aproximación pueden modelizarse mediante un modelo
unidimensional: una cuerda tensa sin rigidez fija en los extremos, o un tubo
acústico delgado: La energía viaja continuamente de un extremo a otro del
instrumento, reflejándose en los extremos una y otra vez, pero sólo permanecen
unos modos de vibración (ondas de
desplazamiento transversal en el caso de una cuerda, o de presión sonora en el
caso del tubo acústico) cuya longitud de onda es una fracción entera de la longitud del
instrumento.
Si el sistema es perfectamente lineal (en el caso de una cuerda esto exige
amplitudes de oscilación muy pequeñas y rigidez despreciable de la misma), las
frecuencias de vibración serán proporcionales al inverso de la longitud de onda
de cada modo de vibración y por tanto múltiplos enteros de la frecuencia
fundamental, que es la correspondiente al modo de mayor longitud de onda.
Matemáticamente se trata de un problema de ecuaciones diferenciales: la ecuación
de ondas unidimensional, con condiciones de contorno homogéneas, la cual tiene
por solución los autovalores del operador laplaciano en el recinto en cuestión.
Como el sonido producido está compuesto de parciales múltiplos enteros de una
frecuencia fundamental, el sonido es agradable por sí mismo, pues una sola nota interpretada por el
instrumento no posea más de un parcial dentro de una misma banda crítica (válido
para los primeros parciales), y además pueden establecerse las importantes relaciones
entre diferentes notas interpretadas por el instrumento que vemos en el apartado
dedicado a la armonía. Cabe
mencionar que si no es por esta organización, ni siquiera los intervalos de
octava tienen fundamento alguno.
Instrumentos que producen un sonido de
tono aceptablemente definido, pero no
aptos para la armonía convencional
Radian la energía concentrada en torno a varios parciales, pero que éstas no
están relacionados mediante relaciones sencillas de números enteros. A este
grupo pertenecen algunos instrumentos de percusión como el xilófono, la marimba,
el carrillón, la celesta,
las campanas tubulares y los timbales.
Los modos de vibración de su estructura no son de un sistema lineal unidimensional,
como en el caso anterior. Las
barras de xilófono poseen múltiples modos torsionales, las barras de la marimba tienen una distribución de masas
muy concentrada en
los extremos, con un tramo central muy delgado, y en los timbales vibra es una membrana
con forma de disco (algunos modos de vibración
estarán por tanto regidos por funciones de Bessel). En estas estructuras, la frecuencia de
vibración de los diferentes modos no guarda ninguna relación sencilla de números
enteros.
Cómo asigna el cerebro un tono virtual a estos sonidos es algo que no se
comprende totalmente; en el apartado de psicoacústica
[tono virtual] indicamos que se basa en la búsqueda de
un mínimo común divisor de los frecuencias de los parciales del centro de la
banda de audición. Además, sabemos que si mediante una
cuidadosa construcción física logramos que aparezca una vibración armónica en la
frecuencia que el cerebro ha asignado al sonido, reforzamos mucho la percepción
del tono. Esto se logra en algunas campanas controlando los modos de vibración
más grave, y en el xilófono y la celesta mediante a
colocación de tubos resonadores debajo de las barras.
Sin embargo, la arbitraria distribución de los diferentes parciales impide
podamos hacer uso de la armonía, válida para los instrumentos musicales del
primer grupo, y que analizamos en el apartado dedicado a la
armonía.
Instrumentos que producen sonidos sin tono
definido
Estos instrumentos, como el gong, el bombo o los platillos, que
irradian su energía de forma muy dispersa, no permiten al cerebro localizar
patrones como envolvente temporal o relaciones entre parciales
armónicos, necesarios para la percepción del tono. Sin embargo, estos
instrumentos pueden generar sonidos potentes, sugestivos, sorprendentes, que
hacen sentir el auditorio "lleno" de sonido, aunque no permiten interpretar
melodías ni construir ningún tipo de armonía con ellos.
Timbre o calidad del sonido
El timbre de los instrumentos de las dos últimas categorías mencionada es un
fenómeno extraordinariamente complejo, debido a la gran variabilidad de la
estructura armónica del sonido, y no podremos, por tanto analizarlo en términos
sencillos.
El timbre de los
instrumentos basados en parciales múltiplos de una fundamental, también tiene
también una gran variabilidad, a pesar de poseer los parciales idénticas
frecuencias. Este fenómeno es debido a la evolución temporal del predominio de
unos u otros parciales.
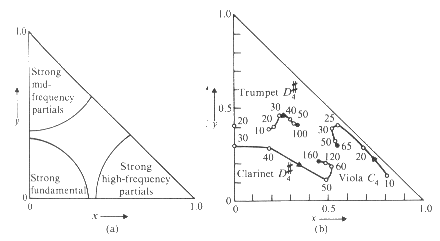
| (a) Explicación del diagrama: la proximidad
a cada vértice del triángulo indica predominio de ciertos parciales |
| (b) Evolución de los sonidos de viola,
trompeta y clarinete |
 |
Existe otro parámetro que modifica el timbre de este tipo de instrumentos:
por ejemplo, en el piano, las cuerdas poseen una cierta rigidez (responsable de
una fuerza recuperadora añadida) que hace que los parciales estén más separados
de lo que les correspondería, mientras que en los instrumentos de viento ocupan
su lugar teórico con gran precisión. Parciales ligeramente desafinados producen
batidos con un resultado similar al
vibrato descrito en
la siguiente sección.
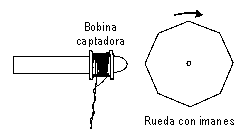 Un
antiguo tipo de órganos electromecánicos
estaá basado en una conjunto de ruedas con imanes que excitaban una bobinas captadoras.
Todas las ruedas giran solidarias al mismo eje, pero cada una posee un diferente
número de imanes (múltiplos de un número fundamental). Ajustando la distancia de
cada bobina a su correspondiente rueda se configuraba el predominio de cada
parcial, con el consiguiente resultado en el timbre.
Un
antiguo tipo de órganos electromecánicos
estaá basado en una conjunto de ruedas con imanes que excitaban una bobinas captadoras.
Todas las ruedas giran solidarias al mismo eje, pero cada una posee un diferente
número de imanes (múltiplos de un número fundamental). Ajustando la distancia de
cada bobina a su correspondiente rueda se configuraba el predominio de cada
parcial, con el consiguiente resultado en el timbre.
Con este instrumento quedó demostrado que parciales afinados con excesiva
precisión quitan solidez al sonido: Como todas las ruedas giran juntas, las
frecuencias de los parciales están exactamente relacionados por números enteros
(el número de imanes en cada rueda), lo que produce un sonido pobre y frío,
debido a la ausencia de los ligeros batidos y modulaciones que
generan parciales no perfectamente afinados.
[Volver al índice]
4.-
Teoría matemática de la comunicación
Existen muchas maneras de codificar información en una señal. La teoría de la
comunicación tiene por objeto el estudio y desarrollo de maneras eficientes de
transmitir la información por un canal. La capacidad máxima de un canal de
comunicaciones fue acotada por Claude Shannon en los años cuarenta, en base a
que la señal no puede variar arbitrariamente rápido –limitación de banda– y
siempre hay un nivel de ruido.
Cuando escuchamos música percibimos claramente la variación en el “tiempo” de la
“frecuencia” de los sonidos. Un sonograma o espectrograma de sonido es un
diagrama tridimensional. En esencia consiste en representar la señal de
sonora (una función unidimensional del tiempo) como una función que depende de
dos variables: tiempo en el eje de abscisas y frecuencia en el eje de ordenadas.
El hecho de que estemos representando una función de una variable como una
función de dos variables implica que existe una ligadura interna en la función,
es decir que no todas las funciones de dos variables serán posibles
representaciones de sonidos. La ligadura interna es la transformada de Fourier.
Esto nos lleva inevitablemente al
principio de incertidumbre, el cual surgió de la mecánica cuántica
debido a que en esta rama de la física la posición de una partícula es una
función del espacio y su cantidad de movimiento (está ligada a la posición) es
la transformada de Fourier de la función de posición.
Dado que funciones muy concentradas en el tiempo tendrán por transformada de
Fourier funciones con componentes de alta frecuencia y señales con componentes
de baja frecuencia cambiarán muy lentamente en el tiempo, nos encontramos con
una limitación, una incertidumbre en la precisión con que queremos conocer la
frecuencia de una señal y lo duradera que esta sea.
A la hora de construir un sonograma necesitamos comprender esta importante
limitación: si queremos realizar el análisis de una señal estacionaria, es
decir, que tiene las mismas características espectrales a lo largo del tiempo
(es como si un clarinete tocase de continuo la misma nota, con la misma
intensidad, durante mucho tiempo), nos bastará con realizar la transformada de
Fourier de la señal temporal al completo, pero de este modo obtendremos una
única función espectral, que será la misma para todo instante de tiempo.
Ahora bien, si queremos analizar un melodía interpretada con rapidez por un
violinista, si realizamos la transformación de Fourier de la pieza al completo
sólo obtendremos una función promedio de las componentes espectrales de la obra.
Necesitamos saber las componentes espectrales que aparecen cuando está sonando
cada una de las notas de la melodía, por lo cual necesitaremos recurrir a una
técnica de ventaneado. El ventaneado consiste en quedarnos sólo con el intervalo
de la función temporal que queramos analizar y hacer cero el resto.
El inconveniente que plantea es que, por las propiedades de la transformada
de Fourier, la función que utilicemos como ventana (para dejar pasar la función
temporal los instantes que nos interesan y bloquearla para el resto) va a
introducir una distorsión en la función espectral resultante, en términos de la
integral de convolución de lo que desearíamos obtener con la transformada de
Fourier de la función ventana. Es decir, según ganamos resolución temporal,
producimos una incertidumbre espectral que nos impedirá distinguir las
componentes armónicas de la función temporal sometida a estudio.
A las funciones que tienen una localización conjunta en tiempo-frecuencia
mínima se les da el nombre de funciones de Gabor.
Se construyen desplazando en tiempo y frecuencia una función concentrada en el
origen (átomo de Gabor). La función más concentrada en el origen resulta
ser la gaussiana, pues el la única función que tiene por transformada de Fourier
a sí misma. Recordamos que por las propiedades de la transformada de Fourier,
desplazar en frecuencia una de estas funciones implica modular la
correspondiente función temporal por una función armónica, de frecuencia
proporcional al desplazamiento frecuencial.
Para desentrañar el contenido de información tiempo-frecuencia, Gabor propuso
descomponer las señales en esas formas de onda atómicas elementales. Demostró la
importancia del procesado de señal localizado en tiempo-frecuencia mostrando que
tales descomposiciones están íntimamente relacionadas con nuestras sensibilidad
a los sonidos, y que exhiben importantes estructuras en las grabaciones de voz y
música.
Construcción de sonogramas
Suelen representarse como una imagen en la que el tono de gris nos indica los
átomos de Gabor en que se descompone la señal.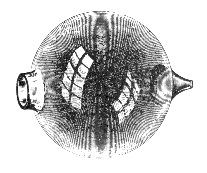
El primer intento de realizar sonogramas fue realizado por Helmholtz, quién
disponía de una gran colección de resonadores acústicos sintonizados en las
diferentes bandas de frecuencias, que le permitieron discriminar con
precisión las componentes espectrales de los diferentes sonidos musicales.
Puesto que necesitaban una gran ganancia, dichos resonadores tenían una gran
persistencia (seguían resonando un tiempo después de que desapareciese la
excitación), por lo que sólo resultaba posible el análisis de sonidos
estacionarios.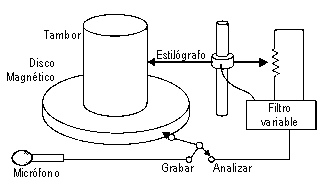
Conservando el mismo esquema de funcionamiento, en los años cuarenta en los
laboratorios Bell fue construido el modelo de sonógrafo de la figura. Un
estilógrafo trazaba sobre un tambor gráficas correspondientes a la respuesta de
una grabación a un filtro pasabanda de banda muy estrecha. Según el estilógrafo
se mueve lentamente de arriba a abajo del tambor, la frecuencia central del
filtro pasabanda va cambiando con la posición. Cada vuelta del tambor
corresponde a una reproducción de la grabación sonora a analizar. La elección
del ancho de banda del filtro nos determinará si deseamos orientar la precisión
del filtro hacia el tiempo o la frecuencia. Sin embargo, si queremos obtener la
reconstrucción de la señal en términos de átomos de Gabor será requisito
imprescindible que la característica de los filtros se aproxime a una Gaussiana,
y que el ancho de banda sea función de la frecuencia en la que esté centrado el
filtro.
Programa Matlab para
generar espectrogramas
Utilizaremos la transformación de Fourier ventaneada. La idea fundamental es
que se elige una función breve lo más regular posible, que llamaremos ventana.
Desplazando esta ventana en el tiempo y en frecuencia obtenemos una
conjunto de funciones que corresponden a una posición dada en el plano
tiempo-frecuencia (rectángulos de Heissenberg), y por tanto pueden representarse
en el sonograma. Para el cálculo de los coeficientes recurrimos a la técnica que
da nombre a esta transformada. Multiplicamos la señal por la ventana y le
realizamos la transformada de Fourier, que resulta ser una columna del
sonograma. Entonces desplazamos la ventana y repetimos el procedimiento,
obteniendo una columna al lado de la anterior. La elección de la ventana es muy
importante, tanto en su tamaño (debe estar acorde a la banda de frecuencias de
interés) como en el tipo de función (elegimos una gaussiana).
function s = wf2(f)
%Fourier ventaneado
f=f';
M=2^15;
%Numero de muestras de la ventana
N=M/2-1;
x=[-(N+1):1:N]./(N+1);
w=exp(-13*x.^2); %Generacion de la ventana
Gaussiana
for k=1:(length(f)-length(w))/(M/16)
s(:,k)=fftshift(fft(f([1:length(w)]+k*(M/16)-1).*w))';
end
ab = [0,length(s(1,:))]/44100*2048; %Vector de abscisas
or = [-22050:22050];
%Vector de ordenadas
image(ab,or,abs(s)*2)
colormap(1-gray);
axis([0,max(ab),-8000,0])
Hay una sonograma obtenido con este programa en el apartado dedicado al
análisis de la armonía música:
"Sonograma de piano tocando la serie de armónicos"
Por último recordamos que un buen sonograma se basa en la descomposición de
la señal en átomos de Gabor. En esencia este análisis sólo se diferencia del
análisis con Fourier ventaneado en el hecho de que las ventanas temporales no
son de tamaño fijo, sino que su tamaño depende de la componente frecuencial que
estén analizando. Así logramos disminuir la incertidumbre temporal en las
componentes de más alta frecuencia, pero no podemos utilizar la transformada de
Fourier para obtener los coeficientes, sino que es necesario recurrir a
herramientas más sofisticadas como son las wavelets analíticas.
Vibrato y modulaciones en
frecuencia/amplitud
El principio de incertidumbre tiene una
importantes implicaciones de cara a la afinación en la interpretación musical.
No importa cuán bien afinada esté una nota si esta suena durante un periodo de
tiempo muy breve, pues la corta duración de la nota nos introduce una dispersión
o incertidumbre en la frecuencia.
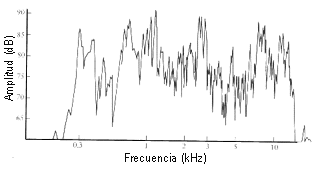 Es
habitual en los intérpretes de violín hacer uso del vibrato, esta técnica
consiste en modular la frecuencia del sonido a un ritmo de 7 Hz. Dado que la
respuesta en frecuencia de la caja del violín es muy áspera y puntiaguda [ver
gráfico], a la modulación en frecuencia que realiza el intérprete hay que añadir
la aparición de una intensa modulación debida al ascenso y descenso de las
crestas de se respuesta en frecuencia. El efecto que estas modulaciones ejercen
sobre el espectro de la nota que suena es la aparición de una dispersión, del
orden de la frecuencia a la que se ejecuta el vibrato, alrededor de cada
armónico del sonido del violín. De esta manera el violinista consigue disimular
pequeñas desviaciones en la afinación, y además proporciona al sonido una gran
sensación de calidez.
Es
habitual en los intérpretes de violín hacer uso del vibrato, esta técnica
consiste en modular la frecuencia del sonido a un ritmo de 7 Hz. Dado que la
respuesta en frecuencia de la caja del violín es muy áspera y puntiaguda [ver
gráfico], a la modulación en frecuencia que realiza el intérprete hay que añadir
la aparición de una intensa modulación debida al ascenso y descenso de las
crestas de se respuesta en frecuencia. El efecto que estas modulaciones ejercen
sobre el espectro de la nota que suena es la aparición de una dispersión, del
orden de la frecuencia a la que se ejecuta el vibrato, alrededor de cada
armónico del sonido del violín. De esta manera el violinista consigue disimular
pequeñas desviaciones en la afinación, y además proporciona al sonido una gran
sensación de calidez.
Respuesta en frecuencia de un sistema amplificador y conservación de la forma de
onda
Llegados a este punto nos encontramos ante una situación relativamente
paradójica que de nuevo enfrenta la periodicidad con la distribución armónica de
un sonido. Dos sonidos pueden tener los mismos parciales, con la misma amplitud
y sin embargo tener una forma de onda muy diferente. Esto es debido a que unos
parciales están desfasados respecto a otros.
La forma de onda afecta al timbre, además, si las diferentes formas de onda
atraviesan un sistema con distorsión, aparecerían mayores diferencias.
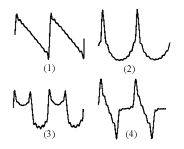
Distinta forma de onda debida a desfase de los armónicos
[4]. Resulta sencillo distinguir las ondas (1) y (2) de
las (3) y (4), pero no la (1) de la (2), ni la (3) de la (4).
|
|
|
(1) sin(wt) + 1/2
sin(2wt) + 1/3 sin(3wt) + . . . + 1/10 sin(10wt) |
|
(2) cos(wt) + 1/2
cos(2wt) + 1/3 cos(3wt) + . . . + 1/10 cos(10wt) |
|
(3) sin(wt) + 1/2
cos(2wt) + 1/3 sin(3wt) + . . . + 1/10 cos(10wt) |
|
4) cos(wt) + 1/2
sin(2wt) + 1/3 cos(3wt) + . . . + 1/10 sin(10wt) |
Para que un amplificador conserve la forma de onda debe tener una respuesta
de fase lineal. Si la respuesta en fase no es constante, aunque sí lineal, se
producirá una variación de las distancias entre armónicos, pero la forma de onda
se conservará.
[Volver al índice]
5.- Teoría de la música / Armonía
Definición de armonía según John R. Pierce: “La armonía la constituyen las
notas que suenan simultáneamente, suave y dulcemente, o las combinaciones de
sonidos duros de notas llenos de tensión, que milagrosamente se resuelven en
un acorde consonante. También lo son las progresiones de acordes que se
utilizan como frases o palabras musicales y la modulación, el paso de una
tonalidad a otra, algunas veces rotunda y otras veces ambigua y esquiva.”
Pitágoras sabía que los sonidos producidos por
varias cuerdas vibrantes suenan
armoniosos cuando sus longitudes mantenían relaciones
sencillas de números enteros. Sin embargo no obtuvo explicación completa del fenómeno.
Galileo (1638) de dio cuenta que en las consonancias agradables existe una
cierta regularidad en la vibración del aire, debido a que “los pulsos
producidos por los dos tonos, al mismo tiempo, deben se conmensurables en
número, de forma que no mantengan al tímpano en un estado de tormento
perpetuo”.
Sin embargo, hasta que en el siglo XIX fueron identificados los diferentes
parciales que componen el sonido que no se obtuvo una explicación convincente
respecto a la naturaleza de estas consonancias.
Para comprender la armonía producida cuando varias notas suenan
simultáneamente, es preciso comprender la
naturaleza del sonido de una única nota producida por un instrumento musical
–su descomposición en términos de armónicos parciales– aspecto que
describimos detalladamente en el apartado dedicado al estudio de la
consonancia/disonancia de un
sonido.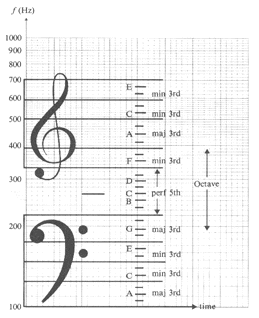
Intervalos musicales
La notación musical occidental, basada en el pentagrama, puede comprenderse como si de un papel milimetrado con el eje de ordenadas (altura del
sonido, frecuencia) en escala logarítmica se tratara. La separación entre líneas
consecutivas corresponde bien a intervalos de tres semitonos (tercera menor), o
de cuatro semitonos (tercera mayor). El eje de abscisas representa el tiempo.
Cada una de las líneas o espacios corresponde a una de las teclas blancas del
piano, mientras que para designar las teclas negras se utilizan alteraciones, a
saber: sostenido # (subir un semitono), bemol b (bajar un semitono).
| Nota: En el
sistema de notación anglosajón las notas se llaman así: |
la |
si |
do |
re |
mi |
fa |
sol |
| A |
B |
C |
D |
E |
F |
G |
Para construir una armonía se necesita una sucesión de sonidos producidos por
un instrumento musical que constituyan la base de las obras musicales que se
interpreten con dicho instrumento, a la cual denominaremos escala musical.
En las escalas musicales, se asocia una nota musical a cada sonido producido
por el instrumento, en función de la altura del sonido. La variable física que
determina la nota es la frecuencia fundamental del sonido (distancia entre
armónicos). Entenderemos por intervalo musical,
la distancia que separa dos notas. Los intervalos musicales pueden medirse en
términos de la relación de frecuencias de los sonidos, aunque en música reciben
nombres propios cuya correspondencia física depende del tipo de escala
utilizada.
Tal y como hemos visto en el apartado anterior, por las propiedades
espectrales de los sonidos, cierto intervalos resultan más consonantes que otros
en virtud de la proximidad entre armónicos aportados por cada una de las notas
que suenan simultáneamente.
En el siguiente sonograma, analizamos el sonido emitido por un piano que toca
las notas más próximas a la serie de armónicos de la nota do1, de frecuencia
fundamental 32.703 Hz. Nos fijaremos en las relaciones de proximidad entre los
armónicos.
Escuchar serie de armónicos

El intervalo de octava resulta muy consonante por la perfecta
coincidencia entre los armónicos. Asimismo, si un sonido es consonante con otro,
también lo será con el sonido una octava más alto, pues este no añade ningún
armónico capaz de producir disonancia. El intervalo de quinta perfecta también
resulta muy consonante pues los armónicos que no coinciden perfectamente,
quedan a la distancia más alejada posible, perfectamente intercalados. En menor
grado esto también es cierto para los intervalo de cuarta perfecta y tercera
mayor y menor. Nos fijamos en estos intervalos exclusivamente, pues como veremos
a continuación son los que utilizaremos como punto de partida para la
construcción de las diferentes escalas.
¿Qué podemos tomar como punto de partida para la construcción de una buena
escala?. La idea esencial es que la escala posea suficientes notas y que los
intervalos entre las ellas sean lo más consonantes posibles, pues al fin y al
cabo las notas de la escala constituyen los ladrillos con los que se construirá
a música a interpretar. En función de a qué intervalos demos mayor prioridad,
surgen muchas maneras de construir escalas. Vamos a estudiar las escalas
justa, pitagórica y de igual temperamento.
La escala de entonación justa (diatónica justa) nace
a partir de la tríada mayor, un grupo de tres notas que suenan
particularmente armoniosas (p.ej. do-mi-sol). El intervalo entre do-mi
es una tercera mayor, entre mi-sol una menor y entre do-sol una quinta
perfecta. La tríada es lo más consonante posible se denomina tríada mayor y
posee relaciones de frecuencias son 4:5:6.
En la escala justa hay tres tríadas mayores, que se denominan acordes de
tónica, de subdominante y de dominante (I, IV y V grado). Están construidas partiendo de las primera, cuarta y quinta notas de la
escala respectivamente.
Para construir la escala justa seguimos el siguiente procedimiento:
Fijamos primero las notas del acorde de tónica (do-mi-sol). Partimos de
do1 normalizado a 1, entonces mi1=5/4 y sol1=6/4=3/2. Ahora procedemos con las notas
del acorde de dominante (sol-si-re), por tanto, si1=3/2*5/4=15/8 y
re2=3/2*3/2 = 9/4, trasponemos este re2 una octava a re1=9/8.
Ahora tomamos el acorde de subdominante (fa-la-do), bajamos desde do2,
a fa1=2/(3/2)=4/3, y a la1=2/(6/5)=5/3.
Desarrollamos las relaciones de la escala justa de do mayor, observándose
tres diferentes relaciones entre notas sucesivas.
| do |
re |
mi |
fa |
sol |
la |
si |
do |
| 1 |
9/8 |
5/4 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
| |
9/8 |
10/9 |
16/15 |
9/8 |
10/9 |
9/8 |
16/15 |
|
| |
Tono entero mayor |
Tono entero menor |
Semitono |
Tono entero mayor |
Tono entero menor |
Tono entero mayor |
Semitono |
|
Aparte de las tres tríadas mayores, la escala justa tiene dos tríadas con las
relaciones 10:12:15, que se denominan tríadas menores. Al igual que las
tríadas mayores, también poseen un intervalo de tercera menor y uno de
tercera mayor, pero cambiados de orden. Es decir, el intervalo más grave
(10/12=6/5) es una tercera menor, y el intervalo más agudo (15/12=5/4) es
una tercera mayor.
Problemas de la escala justa
Las quintas en la escala justa no son todas iguales: son perfectas
(3/2) todas menos una (re-la). Una de las cuartas tampoco es
perfecta (la-re). tas
son perfectas, la-re no lo es. Si añadimos alteraciones
(sostenidos y bemoles), encontramos el problema de que si requerimos que mi-sol# sea una tercera mayor, entonces
G# =5/4*5/4=25/16, pero si requerimos
que lab-do sea una tercera mayor, entonces lab=2/(5/4)=8/5. Es
decir, lab es un poco más aguda que sol#.
Sin embargo, en el piano para sol# y lab hay una única tecla; son las
llamadas notas enarmónicas.
La construcción de instrumentos afinados en la escala justa no es muy
práctica porque requeriría complicados teclados para las enarmonías
mencionadas anteriormente y haría falta volver a afinar el instrumento
completamente cada vez que se desease cambiar de tonalidad.
La escala pitagórica se basa en la creación del mayor número posible de
cuartas y quintas perfectas. Para conseguirlo, sacrificamos la afinación
terceras mayores y menores, así como las sextas, respecto la entonación justa.
-
Una octava es una cuarta más una quinta (4/3*3/2=2), por tanto,
subir una cuarta es lo mismo que basar una quinta y viceversa.
-
Todas las notas de la escala (incluidos sostenidos y bemoles), pueden
alcanzarse subiendo o bajando 12 quintas o doce cuartas sucesivamente.
Para construir la escala pitagórica vamos ascendiendo en intervalos
de quintas justas (do1-sol1-re2-la2-mi3-si3; luego traspondremos las
notas a la octava apropiada), si continuamos el proceso obtenemos los sostenidos
y ascendiendo cuartas justas, obtendríamos los bemoles. La escala pentatónica
surge naturalmente mediante es procedimiento constructivo; basta detener el
proceso una vez obtenidas cinco notas.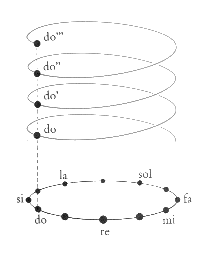
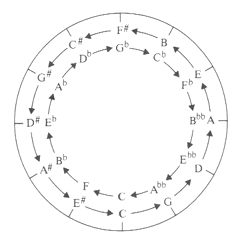
Sin embargo, si continuamos el procedimiento para obtener los
sostenidos y bemoles, encontramos relaciones como las resultante entre fa#-fa
es 2187/2048=1.068 (la denominaremos semitono cromático), que es menor
que el semitono diatónico (156/143=1.053) que aparece entre notas
sin alteraciones.
Si continuamos el proceso 12 veces intentando llegar a la misma
nota de partida y así cerrar el círculo después de obtener todas las posibles
notas alcanzamos la relación 3/2^12=129.7, próxima a siete octavas, pero con un
error acumulado que nos aparta de nuestro objetivo, las siete octavas 2^7=128.
Este intervalo resultante, que nos aparta de nuestro objetivo se denomina
coma pitagórica, y es igual al intervalo que separa un semitono cromático de
un semitono diatónico, el intervalo que separa notas enarmónicas.
Desarrollamos las relaciones de la escala pitagórica de do mayor,
la cual tiene una única relación de tono, pero dos de semitono.
| do |
re |
mi |
fa |
sol |
la |
si |
do |
| 1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/16 |
243/128 |
2 |
| |
9/8 |
9/8 |
256/243 |
9/8 |
9/8 |
9/8 |
256/243 |
|
La principal ventaja de la escala pitagórica es el que las cuartas y las quintas
son siempre prefectas. Sin embargo, las terceras tienen una afinación muy
pobre. La relación por la cual las tercera mayores exceden y las terceras
menores quedan por debajo de las terceras justas, es 1.0125,
denominado coma sintónico.
También resulta interesante saber que muchos cantantes y violinistas tienden en favor de la
entonación pitagórica en sus interpretaciones, lo que ratifica la
importancia de las quintas y cuartas en la música.
Las afinaciones temperadas
parten de la escala pitagórica, con la idea de alterar algunas notas en
fracciones de coma
sintónico antes mencionado, con el fin de acondicionar un poco las
terceras, que suenan desafinadas.
La escala de temperamento de tono medio de cuarto de coma sube o baja
varias notas en fracciones 1/4, 1/2, 3/4 o 5/4 del coma sintónico (el valor
por el cual las terceras mayores y menores difieren de sus valores justos
correspondientes). Sin embargo, entendemos que no se trata más que de una aproximación a la afinación
más ampliamente utilizada en los instrumentos musicales:
La escala de igual temperamento, habitualmente denominada escala
temperada se basa en que todos los semitonos sean idénticos (lo que implica
también tonos idénticos). Una octava está formada por doce semitonos, o bien
cinco tonos y dos semitonos.
La relación del semitono de igual temperamento es igual a
2^(1/12) = 1.05946.
El tono corresponde a 1.05946^2=1.12246. La quinta es 1.498 y la cuarta es 1.335, ambas muy próximas a los intervalos
perfectos 1.500 y 1.333. La tercera mayor es 1.260 y la tercera menor
1.189, no están demasiado próximas a los intervalos justos 1.250 y 1.200, pero
tampoco están tan desafinados como las terceras de la escala pitagórica.
En lugar de trabajar con relaciones de frecuencias, es habitual comparar las
notas
utilizando cents. Un cent es 1/100 de un semitono de igual temperamento. Por
tanto, una octava son 1200 cents, una quinta temperada 700 cents, una cuarta
temperada 600 cents, y así sucesivamente. Un cent corresponde a la relación 2^(1/1200)=1.000578.
La principal ventaja de la escala de igual temperamento reside en que todas
las notas enarmónicas poseen la misma afinación (imprescindible para la
construcción de los instrumentos musicales), y que no es necesaria ninguna
afinación para interpretar obras en diferentes tonalidades.
Tabla comparativa de los principales intervalos en las
escalas temperada, justa y pitagórica:
|
Intervalo |
Temperada |
Justa |
Pitagórica |
|
Relación |
Cents |
Relación |
Cents |
Relación |
Cents |
|
Octava |
2.000 |
1200 |
2/1 = 2.000 |
1200 |
2.000 |
1200 |
| Quinta |
1.498 |
700 |
3/2 = 1.500 |
702 |
1.500 |
702 |
| Cuarta |
1.335 |
500 |
4/3 = 1.333 |
198 |
1.333 |
498 |
| Tercera mayor |
1.260 |
400 |
5/4 = 1.250 |
386 |
1.265 |
408 |
| Tercera menor |
1.189 |
300 |
6/5 = 1.200 |
316 |
1.184 |
294 |
| Sexta mayor |
1.682 |
900 |
5/3 = 1.667 |
884 |
1.687 |
906 |
|
Sexta menor |
1.587 |
800 |
8/5 = 1.600 |
814 |
1.580 |
792 |
[Volver al índice]
Referencias
[1] TASAKI, I. (1954). Nerve Impulses in
Individual Auditory Nerve Fibres. J. Neurophysiology 17:97
[2] ERICKSON, R. (1975). Sound Structure
in Music. Berkeley: University of California (capitulo 2)
[3] PLOMP, R., y W. J. M. LEVELT (1965).
Tonal Consonance and Critical Bandwidth. J. Acoust. Soc. Am. 38:548
[4] PLOMP, R., Y H. J. M.
STEENEKEN (1969). Effect of Phase on the Timbre of Complex Tones. J. Acoust. Soc.
Am. 46:409
[Volver al índice]
- ROSSING, Thomas D. The Science of Sound, 2ª ed. Addison-Wesley
Publishing Company, 1989.
- PIERCE, John R. Los sonidos de la música, 1ª ed. Scientific Ameican
Books, 1985.
- HELMHOLTZ, H. L. F. von (1877). On the Sensations of Tone as a
Physiological Basis for the Theory of Music, 4th ed. Trans., A. Mendel.
New York: Associated Music Publishers, 1945.
- BÉKÉSY, Georg von, Experiments in Hearing, 1960
[Volver al índice]


 En este apartado vamos a seguir el camino y transformaciones de la señal
auditiva desde que incide en el tímpano hasta que recorre el nervio auditivo
camino del cerebro.
En este apartado vamos a seguir el camino y transformaciones de la señal
auditiva desde que incide en el tímpano hasta que recorre el nervio auditivo
camino del cerebro.








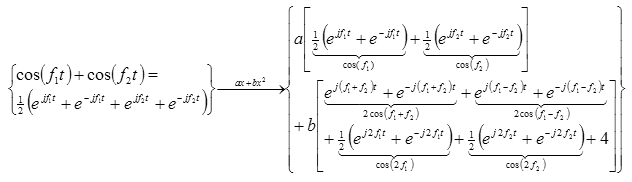



 Un
antiguo tipo de
Un
antiguo tipo de 

 Es
habitual en los intérpretes de violín hacer uso del vibrato, esta técnica
consiste en modular la frecuencia del sonido a un ritmo de 7 Hz. Dado que la
respuesta en frecuencia de la caja del violín es muy áspera y puntiaguda [ver
gráfico], a la modulación en frecuencia que realiza el intérprete hay que añadir
la aparición de una intensa modulación debida al ascenso y descenso de las
crestas de se respuesta en frecuencia. El efecto que estas modulaciones ejercen
sobre el espectro de la nota que suena es la aparición de una dispersión, del
orden de la frecuencia a la que se ejecuta el vibrato, alrededor de cada
armónico del sonido del violín. De esta manera el violinista consigue disimular
pequeñas desviaciones en la afinación, y además proporciona al sonido una gran
sensación de calidez.
Es
habitual en los intérpretes de violín hacer uso del vibrato, esta técnica
consiste en modular la frecuencia del sonido a un ritmo de 7 Hz. Dado que la
respuesta en frecuencia de la caja del violín es muy áspera y puntiaguda [ver
gráfico], a la modulación en frecuencia que realiza el intérprete hay que añadir
la aparición de una intensa modulación debida al ascenso y descenso de las
crestas de se respuesta en frecuencia. El efecto que estas modulaciones ejercen
sobre el espectro de la nota que suena es la aparición de una dispersión, del
orden de la frecuencia a la que se ejecuta el vibrato, alrededor de cada
armónico del sonido del violín. De esta manera el violinista consigue disimular
pequeñas desviaciones en la afinación, y además proporciona al sonido una gran
sensación de calidez.