| Ecografías 2D |
|
||
|
En 1965 La firma Kretztechnik junto con el Dr Werner Buschmann, fabricó un transductor de 10 elementos dispuestos en fase, para examinar el ojo. En 1968, Sommer desarrolló scanner electrónico con 21 cristales de 1.2 MHz, que producía 30 imágenes por segundo. |
Si en la sonda sólo hay un elemento activo, tan sólo podemos obtener información de una línea, salvo que ese elemento sea móvil. La movilidad del elemento podría ser una solución para obtener información de varias lineas (y formar un plano), pero para las ecografías Doppler esto puede suponer un problema.[8]
Como solución se emplean varios transductores, es lo que se conoce como "array de transductores". La disposición de los elementos activos en el array hace que la información recibida sea diferente. El apartado El ecógrafo" ya se indicaron varios tipos de arrays, en este se indican varios tipos de sondas.
Cada elemento activo emite un pulso hacia un objeto en un instante determinado. Las líneas correspondientes a pulsos consecutivos se muestran en pantalla una junto a la otra formando una imagen 2D.
Se incluye además un apartado dedicado al procesamiento de la imagen en el que se trata la técnica de contornos activos así como alguna técnica para mejorar la resolución.
Obtención de la información bidimensional:
Como ya se ha explicado en el apartado relativo al ecógrafo, para recoger información acerca de un punto (en realidad un pequeño volumen), es necesario un transductor. Estos transductores podemos identificarlos con las sondas. Veamos un pequeño esquema de una sonda:
Hay muchos tipos de sondas, cada una para una aplicación específica. A continuación veremos sólo algunos de los más comunes.
Tipos de sondas bidimensionales:
En el apartado sobre el ecógrafo se ha hablado de tipos de transductores, por tanto puede parecer que este apartado es redundante, pero no lo es. El el apartado tipos de transductores se habla de ellos de modo técnico, mientras que en este se hablará en un tono médico.[12]
1.- Sonda lineal:
-
Proporcionan un formato de imagen rectangular.
-
Se usan para el estudio de estructuras más superficiales como: Músculos, tendones, mama, tiroides, escroto, vasos superficiales, etc.
-
Al usarse para la exploración de estructuras más superficiales las frecuencias de trabajo suelen ser entre 7.5 y 13 MHz, aunque existen hasta 20 MHz.
-
Ejemplo de imagen obtenida con este tipo de sonda:
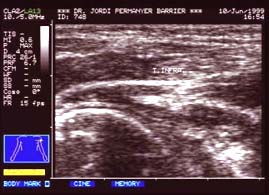
2.- Sonda sectorial:
-
Proporcionan un formato de imagen triangular o en abanico con una base de inicio de la emisión de los ecos mínima.
-
Se usan en la exploración cardiaca y abdominal ya que permiten tener un abordaje intercostal.
-
Al usarse para la exploración de estructuras más profundas su frecuencia de trabajo suele ser entre 3.5 y 5 MHz.
-
Ejemplo de imagen obtenida con este tipo de sonda:

3.- Sonda convex:
-
Tienen una forma curva y proporcionan un formato de imagen de trapecio.
-
Se usan en la exploración abdominal general y obstétrica.
-
Las frecuencias de trabajo son las mismas que en las sondas sectoriales.
-
Ejemplo de imagen obtenida con este tipo de sonda:

4.- Sonda intercavitaria:
-
Pueden ser lineales y/o convex.
-
Se usan para exploraciones intrarectales e intravaginales.
-
Las frecuencias de trabajo suelen ser entre 5 y 7.5 MHz
-
Ejemplo de imagen obtenida con este tipo de sonda:

APLICACIÓN: Cálculo del tamaño de un órgano: Procesamiento de la imagen.
Una de las aplicaciones más utilizadas en el diagnóstico por imagen es la del cálculo de volumen, para ello se genera un volumen de revolución a partir del contorno del órgano en cuestión. Para obtener el contorno hay muchas técnicas, pero quizá la más utilizada es la de los contornos activos. En esta técnica se genera una curva cerrada y se deforma para que se aproxime al contorno real.
A simple vista vista puede parecer sencilla la obtención del contorno, pero no lo es en absoluto. Son muchos los estudios llevados a cabo para mejorar la verosimilitud, ya que en la propagación de cualquier onda se superpone un proceso aleatorio que en este caso distorsionaría la imagen, es lo que se conoce como efecto Speckle.
La forma de reconstruir una contorno es la que se muestra a continuación:
Supongamos que el órgano que se desea inspeccionar tiene una forma parecida a la de la figura sobre estas líneas, por ejemplo un riñón.
(NOTA: La señal recibida es discreta, y sin embargo el contorno debe de ser continuo, este problema se resuelve creando una función continua a partir de las muestras discretas.)
En primer lugar, el ecógrafo no va a mostrar una imagen tan nítida, sino que presentará picos debidos al ruido. La pregunta está en ¿debe el ecógrafo eliminar esos picos, es decir, la función que representa el contorno asociada al órgano debe ser lo más regular posible?. En principio si, pero ¿y si el órgano presenta una forma como la que se muestra en la siguiente figura?.
La respuesta es clara, la función de contorno debe ajustarse al contorno que se indique mediante muestras, pero debe ser lo más suave posible, se impone el criterio de suavidad del contorno. Esta técnica que utiliza los datos recibidos de la imagen e información a priori (suavidad del contorno), es conocida como técnica de contornos activos.
Técnica de contornos activos o Snakes, filosofía Bayesiana:
Desde que fueron introducidos por Kass y sus colaboradores, los contornos activos o snakes se han convertido en una herramienta eficaz en numerosas tareas relacionadas con el procesamiento y el análisis de imágenes como pueden ser entre otras la segmentación y el seguimiento de objetos móviles o su deformación.
Los contornos activos se definen como curvas elásticas que se deforman para adaptarse a las características destacables de una escena respondiendo de un modo natural a las fuerzas ejercidas sobre ellos. Constituyen técnicas de análisis de imágenes en base a modelos que pueden llevas a cabo variaciones de su forma más allá de simples transformaciones, rotaciones o escalado. Dependiendo del tipo de representación que se adopte para su geometría podrán experimentar deformaciones con mayor o menor complejidad y/o libertad: elipsoides, splines (curvas interpolatorias), elementos finitos, poligonizaciones, etc. El modelado de sus propiedades elásticas permite incorporar información a priori (Teorema de Bayes) sobre la forma deseada. El modelo más simple es el que impone las características de continuidad y suavidad de la curva. Hay otros que penalizan deformaciones que lo alejan de lo que se puede considerar su forma natual, o que violan ciertas condiciones de simetría. Dichas restricciones implícitas en un modelo de snake son de carácter débil a diferencia de lo que ocurre en otras estrategias de modelos deformables estríctamente paramétricos como las técnicas basadas en plantillas deformables.[1][4]
Los snakes representan un caso particular dentro de la teoría general de modelos deformables multidimensionales Sus principales características son:
-
Capacidad para manejar información extraída de la imagen tanto de carácter local como global, lo que les confiere mayor robustez ante imágenes con información dispersa y/o incompleta.
-
Posibilidad de incorporar información extraída del conocimiento a priori sobre las estructuras a delimitar, lo que les dota de mayor robustez ante ruido y bajo contraste.
Bajo estas líneas vemos la segmentación de una imagen tomográfica de una sección transversal de la tibia y el peroné mediante la técnicas de detección de borde (izda.) y contornos activos (dcha.) Se puede apreciar que la segunda imagen presenta un aspecto mejor que la primera.


Podemos concluir que para obtener una imagen ecográfica bidimensional no sólo hay que recoger y ordenar información, sino que también debemos aportar información a priori para paliar efectos del ruido y ausencia de información en determinados puntos. Es decir, sin el correspondiente procesamiento de la imagen los resultados serían de muy baja calidad.
Para conocer la resolución en imágenes obtenidas en modo B (señal modulada en brillo. Véase apdo. El ecógrafo) hay que diferenciar dos tipos:
1.- Resolución axial: Es la resolución en la dirección de propagación del haz, y viene determinada por la longitud del pulso de ultrasonido transmitido. Ésta viene dada por:

Donde
![]() es
la duración del pulso y c es la velocidad de fase. En la práctica, la
resolución axial está limitada a dos o tres veces la longitud de onda de la
portadora
es
la duración del pulso y c es la velocidad de fase. En la práctica, la
resolución axial está limitada a dos o tres veces la longitud de onda de la
portadora
PROBLEMA: Si la distancia (en la dirección de propagación del haz) entre dos interfases es inferior a la longitud del pulso, los ecos procedentes de ambas se solapan y no se pueden diferenciar, se interpretan por tanto como uno solo.
2.- Resolución lateral: Es la resolución en la dirección perpendicular al haz y viene determinada por su anchura. Un ecógrafo convencional muestra los ecos de cualquier estructura que se encuentre dentro de la zona de recepción del haz de igual manera que si estuviese en el eje del haz. Esta resolución depende del enfoque del haz y puede variar mucho a lo largo del eje. Normalmente es menor que la resolución axial (varias longitudes de onda de la portadora)
Los dos tipos de resolución determinan lo que se conoce como "celda de resolución". Los ecos procedentes de cualquier estructura que se encuentre dentro de la celda se va a superponer al ser recibidos y no va a ser posible distinguirlos. Este hecho es el responsable de la naturaleza ruidosa de las imágenes de ultrasonidos.[1][8]
Método para aumentar la resolución aumentando la frecuencia:
Aunque propiamente no se pueda considerar una técnica de procesado de imagen, se ha incluido en este apartado por ser un método sencillo de mejorar la calidad de la misma.
El radio de enfoque (radio de la circunferencia que proyecta una fuente al incidir sobre una superficie no transparente a esa onda) de una onda es proporcional a la longitud de la onda. Es decir, aumentando la frecuencia (disminuyendo longitud de onda) podemos conseguir un "punto" más fino, es decir, concentramos toda la energía en menos superficie. Esto provoca que el receptor reciba información más nítida sobre un punto, ya que siempre se recibe información acerca de un pequeño volumen, pues no se puede enfocar un sólo punto, no existe el enfoque perfecto. Veamos una tabla con valores típicos de resolución dependiendo de la longitud de onda:[1]
| Frecuencia (MHz) | Resolución Axial (mm) | Resolución Lateral (mm) |
| 3.0 | 1.1 | 2.8 |
| 4.0 | 0.8 | 1.5 |
| 5.0 | 0.6 | 1.2 |
| 7.5 | 0.4 | 1.0 |
| 10.0 | 0.3 | 0.2 |