| Speckle |
| Índice: (Haga click sobre ellos para acceder a la sección correspondiente) |
| ►Introducción. |
| ►Modelos de speckle. |
| ►Speckle completamente formado. |
| ►Speckle completamente resuelto. |
| ►Speckle parcialmente formado. |
| ►Speckle parcialmente resuelto. |
|
|
|
||
|
John William Strutt, Lord RAYLEIGH (1842 - 1919)
|
El speckle es el patrón de interferencia que se forma cuando una imagen se obtiene a partir de la iluminación de un medio con una radiación no coherente y la posterior detección no coherente (detector de envolvente), cuando el medio contiene una distribución aleatoria de dispersores dentro de la celda de resolución. Estos elementos dispersores surgen de las irregularidades y estructuras microscópicas que son más pequeñas que la celda de resolución. El speckle se puede considerar como ruido, sin embargo, también se puede considerar que aporta información sobre la estructura interna del tejido.
La señal a la entrada del receptor de envolvente es el resultado de la suma de los ecos procedentes de los elementos dispersores. Tiene, por tanto, características aleatorias por estar formada por la suma de señales procedentes de elementos situados en en posiciones aleatorias. Es posible que algunos de estos elementos presenten cierta periodicidad en su colocación, lo que provoca la aparición de una componente determinista en la señal. Las reflexiones especulares, más fuertes que los ecos procedentes de la dispersión, también contribuyen con componentes deterministas. Podemos afirmar que la señal recibida está formada por componentes aleatorias y componentes deterministas.
Para la recepción se utiliza un detector de envolvente (no coherente), por tanto se pierde la fase de la señal. Si la distribución espacial de los dispersores es completamente aleatoria, la fase es una función aleatoria uniforme, por lo que el hecho de descartar la fase de la señal recibida no supone una pérdida importante de la información. Se analizarán las envolventes.
Es importante recordar un teorema asintótico, Teorema del Límite Central que decia: "La distribución de la suma de un número elevado de variables tiende a comportarse como la distribución de una variable gaussiana, tanto más cuantas más variables intervengan en la suma". Este teorema se aplica cuando las variables involucradas son independientes, aunque esta condición puede relajarse en ciertos casos. Nótese que hay las versiones más exigentes del teorema requieren no sólo la independencia de las variables, sino la idéntica distribución, variables IID. Pero esta última condición puede relajarse si ninguna de las variables predomina sobre el resto. Las siguientes figuran muestran la convergencia hacia una distribución gaussiana (línea discontinua) a partir de variables aleatorias uniformes u(0,1). En cada imagen se han ido añadiendo más variables aleatorias, se empieza con una y se finaliza con 10.[9]
También es importante recordar que toda señal puede descomponerse en envolvente y fase. Si la señal original tiene distribución gaussiana, la fase la tendrá uniforme y la envolvente de Rayleigh. Esto es muy importante, ya que en virtud del teorema antes citado podemos modelar la señal recibida como una gaussiana.
- Speckle completamente formado:
Se produce cuando el número efectivo de dispersores en la celda de resolución es grande. La región de dispersión es muy accidentada comparada con la longitud de onda y la estructura de dispersión es demasiado fina para ser resuelta. No hay componente determinista. Utilizando notación fasorial, la señal recibida es una suma de fasores de amplitud y fases aleatorias, que giran a una frecuencia angular Wo, Si cada dispersor refleja un eco de amplitud Xn, que llega al receptor con una fase Φn, la señal recibida viene dada por:

Si Xn y Φn son independientes, la fase de Zx está uniformemente distribuida en (-π, π), y si el número de dispersores dentro de la celda de distribución N es muy grande, la densidad de probabilidad de la envolvente X sigue una distribución de Rayleigh: (En la figura f.d.p de Rayleigh para σ = 1)


Donde E{X2}=2σ2 es la potencia total dispersada hacia el receptor.
- Speckle completamente resuelto:
Se da la misma hipótesis del modelo anterior, que el número de dispersores presentes en la celda de resolución es muy grande, pero en este caso tenemos la presencia de una componente determinista junto con la componente aleatoria. Como ya hemos dicho, dicha componente determinista puede tener su origen en que los dispersores estén situados siguiendo un patrón de periodicidad espacial o en el que existan fuertes reflexiones especulares. El fasor correspondiente a la señal recibida es:

Donde Zs es el fasor correspondiente a la componente determinista de la señal (s). La distribución que presenta la envolvente X es de Rice: (En la figura f.d.p de Rice para σ = 1)

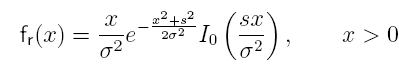
Nótese que si s=0 , no hay componente determinista, la distribución sería de Rayleigh. Por tanto, la distribución de Rayleigh puede considerarse un caso particular de la distribución de Rice. Cabe destacar también que cuando aumente mucho la componente determinista respecto de la aleatoria, la distribución de Rice se comporta como una Gaussiana de media s y de varianza σ2 .
- Speckle parcialmente formado:
Cuando el número de dispersores es elevado y no hay componente determinista el modelo de Rayleigh es el adecuado, sin embargo, si el número efectivo de dispersores es pequeño (número efectivo de dispersores es función del número del número de dispersores existentes en la celda de resolución y del coeficiente de retrodispersión de dichos dispersores), el modelo de Rayleigh deja de ser adecuado. La envolvente sigue una distribución K que tiende a la distribución de Rayleigh cuando el número efectivo de dispersores tiene a infinito. El fasor de la envolvente recibida es:

Función de densidad de probabilidad K en función del número efectivo de dispersores α con σ = 1.

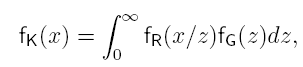
![]()
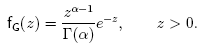

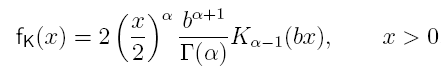
- Speckle parcialmente resuelto:
El modelo de distribución K supone una generalización de la distribución Rayleigh, que considera la posibilidad de tener densidades de dispersores pequeñas. Sin embargo, no tiene en cuanta la presencia de una componente determinista en la señal recibida. Por el contrario, la distribución de Rice es una generalización de la distribución de Rayleigh, que sí tiene en cuenta la presencia de componente determinista, pero que no es válida cuando el número de dispersores es pequeño. Para construir un modelo totalmente general que tenga en cuenta la posibilidad de que el número efectivo de dispersores sea pequeño y que considere la presencia de una componente determinista en la señal recibida, se ha de recurrir a la distribución K homodina. El fasor de la señal recibida es:

Su f.d.p. es K homodina:

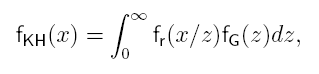
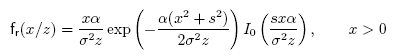
(Extracto de [8])