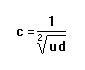
Sonido y mar
Velocidad del sonido en el mar
Un parámetro importante es la celeridad, es decir el valor escalar de la velocidad. Tratandose del agua del mar la propagación se realiza mediante ondas esféricas y en todas direcciones.
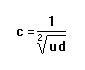
Donde:
c: Celeridad.
u: Coeficiente de compresibilidad.
d: Masa específica.
Pero el coeficiente de compresibilidad del medio varía con la profundidad, mientras que la masa específica depende de la temperatura y salinidad del agua.
La celeridad con la que el sonido de propaga en el mar no es uniforme,los rayos sonoros (las trayectorias que siguen los frentes de ondas), dependen de este hecho.
Teniendo esto en cuenta se puede dar un valor de la velocidad gracias a la ecuación empírica:
![]()
Donde:
c: Velocidad del sonido en m/s.
T: Temperatura del agua en grados centígrados.
S: Salinidad expresada en tanto por mil.
d: Profundidad con relación a la superficie del mar en m.
Se considera generalmente una velocidad estándar para estudiar los fenómenos de propagación de 1450 m/s. También suele adoptarse una impedancia carácteristica estándar de 1'54 millones de rayls.
Como consecuencia de la variación de la celeridad en el plano vertical, podemos decir que el mar se haya estratificado en zonas, en cada una de las cuales los rayos sonoros terdrán distinto comportamiento. Para estudiar las estratificaciones se les asigna un valor por cada una de las variables que intervienen llamados gradientes, y que se obtienen mediante la relación entre la diferencia de valores de la variable y la diferencia de valores en la función.
Traza baticelerimétrica
La representación gráfica de los valores de celeridad y/o temperatura y profundidad se conoce como "TRAZA BATICELERIMETRICA".
Viendo la "traza" puede comprobarse que el océano está dividido en capas verticales o estratificaciones en razón al gradiente en cada una de ellas. Básicamente en todos los mares se da el mismo fenómeno por lo cual puede decirse que la traza se encuenta dividida en cuatro zonas:
- Zona 1, Capa superficial o de mezcla:
Abarca desde la superficie hasta los 50 mts., donde se deja sentir el calentamiento debido a la radiación solar y los efectos meteorológicos.- Zona 2, Termoclina estacional:
Presenta un gradiente negativo cuya intensidad varía con la época del año. En verano y otoño suele ser muy pronunciada porque las aguas superficiales son muy cálidas pero en primavera e invierno puede confundirse con la capa de mezcla.- Zona 3, Termoclina permanente:
Abarca desde el final de la termoclina estacional hasta los 1.600 mts. aproximadamente. Presenta un gradiente negativo suave y uniforme de temperatura. Se ve poco afectada por los cambios estacionales.- Zona 4, Isoterma profunda:
Abarca desde los 1.600 mts. hasta el fondo. La temperatura permanece constante y la celeridad aumenta con la profundidad.
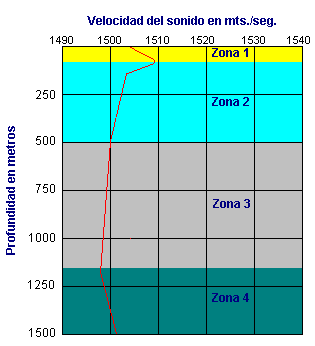
El punto de la traza en el que se da la máxima temperatura a la mayor profundidad se denomina profundidad de capa, y tiene una especial importancia en la propagación del sonido.
En el aspecto horizontal no existen variaciones de presión, las de salinidad suelen ser mínimas y las de temperatura pequeñas en comparación con las del plano vertical, por lo que la traza horizontal no se considera habitualmente.
Propagación
La superficie radiante de un emisor submarino al vibrar, induce a las partículas del medio a desplazarse de sus posiciones de reposo. Dentro del límite de elasticidad del medio, las vibraciones del emisor, pueden transmitirse a grandes distancias, ya que las partículas adyacentes provocan perturbaciones sucesivas de modo que la señal emitida se transmite en forma de ondas que se alejan de la fuente.
La ecuación diferencial fundamento de la acústica ondulatoria que gobierna la propagación de las ondas es:
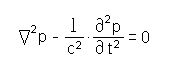
Donde:
c: Valor de la celeridad en el punto (x,y,z).
p: Presión.
t: Tiempo.
Modelos de propagación
El punto de partida de todos los modelos es la ecuación de ondas para una fuente puntual. Hay dos aproximaciones a la solución de la ecuación de ondas: modos normales y rayos.
- Modos normales:
Calculan la integral de la ecuación de ondas o la expanden en función de un conjunto finito de "modos normales". Cada uno de estos modos supone que la solución de la ecuación es el producto de una función dependiente de la profundidad y de una función dependiente del alcance.
El modelo físico que impone es la suposicón de que tanto las superficie como el fondo sean perfectamente planos y que el medio de propagación sea homogéneo, lo cual no es exacto en el mar. Además la búsqueda de soluciones exactas a la ecuación de ondas es matemáticamente compleja y difícil de interpretar.- Rayos:
Se basa en el supuesto de que la energía sonora es transmitida a lo largo de trayectorias (rayos) que son líneas rectas en todas las partes del medio en que la velocidad del sonido es constante, y líneas curvas, de acuerdo con las leyes de refracción donde la velocidad del sonido es variable.
Para entender lo que es un rayo sonoro, supongamos una fuente sonora omnidireccional que vibra produciendo ondas esféricas. La superficie de la esfera cuyos puntos vibran con lamisma fase es el denominado 'frente de onda'. Si nos fijamos en la dirección en que la energía fluye, hay que pensar en un conjunto infinito de radios que surgen del centro de la fuente. Estos radios son los llamados 'rayos sonoros' y son en todo momento perpendiculares a los frentes de onda generados.
El modelo de rayos presenta una solución menos compleja y de fácil interpretación visual, pero tiene las siguientes restricciones de aplicación:1.Cuando los radios de curvatura de los rayos son mayores que la longitud de onda.2.Cuando la velocidad del sonido varía apreciablemente a lo largo de distancias inferiores a la longitud de onda.Por estos motivos el empleo de los MODOS NORMALES se reduce a aquellas frecuencias en que los RAYOS no pueden dar soluciones efectivas, a frecuencias inferiores a 300 Hz.
La siguiente tabla muestra las diferencias entre ambos modelos.
| Modos normales | Rayos |
|---|---|
| Solución teórica completa | Sin solución para el problema de difracción |
| Presentación poco intuitiva | Presentación visualmente interpretable |
| De difícil aplicación para rebotes en superficie o fondo | Fácil aplicación para rebotes |
| Válido para todas las frecuencias | Válido solo a altas frecuencias |
| Dependiente de la fuente | Independiente de la fuente |
| Solución matemática compleja | Solución matemática sencilla |
Fenómenos de refracción y reflexión
La trayectoría de una onda acústica a través de un medio en el que la velocidad varía con la profundidad se puede calcular mediante la aplicación de la ley de Snell:
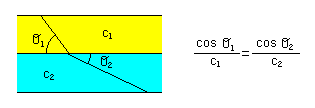
Donde:
c1: Celeridad en la capa superior.
c2: Celeridad en la capa inferior.
O1: Angulo de entrada del rayo en la capa inferior.
O2: Angulo de salida del rayo en la capa inferior.
Puede demostrarse que la trayectoria de una onda acústica a través del agua que tiene un gradiente de velocidad constante u positivo de g m/s es un arco de circunferencia. Consideramos un circulo de radio R según se ve en la figura:
A partir de esta figura tenemos:
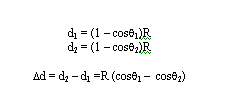
Como el agua tiene un gradiente de velocidad constante y positivo, la velocidad del sonido disminuye con la profundidad:
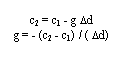
A partir de la ley de Snell y esta última ecuación tenemos:
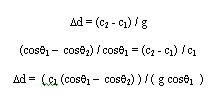
Comparando esta ecuación con la siguiente, vemos que la trayectoria es circular y su radio vale:
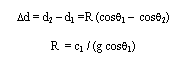
Trayectorias sonoras
La trayectoria de un rayo sonoro al abandonar el emisor depende principalmente de:
- El ángulo de salida del emisor.
- La velocidad de propagación.
- La posición del emisor.
Las zonas en las que la celeridad es constante los rayos que salen del emisor se comportan como líneas rectas.
El receptor recibirá rayos directos e indirectos (debidos a rebotes), cuyo instante de llegada dependerá del camino que hayan recorrido.
Suponiendo una superficie y un fondo planos:
- Si el emisor y el receptor están cerca de la superficie deprecio los rayos que inciden sobre esta.
- Si ambos están situados a una profundidad media, estos rayos si deben ser tenidos en cuenta.
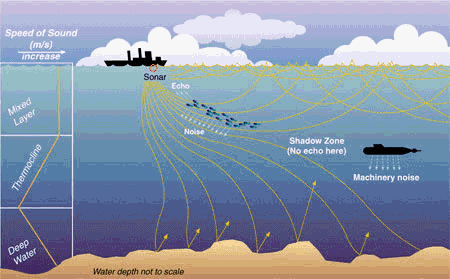
Canales sonoros
Estudiaremos la refracción a grandes profundidades donde la temperatura es casi constante, unos 4 grados centígrados. Allí las condiciones son bastante estables y uniformes todo el año.
En este caso la velocidad del sonido alcanza un mínimo, aumentando a menores profundidades por el incremento en la temperatura y a mayores profundidades por el incremento de la presión.
Los rayos que se originan en esta región de velocidad mínima forman un pequeño ángulo con la horizontal tendiendo la curva a volver hasta este nivel sin alcanzar otra superficie o el fondo, formando un canal sonoro.
Propagación de rayos acústicos en un canal sonoro.
Para analizar este tipo de transmisión suponemos que:
- La velocidad aumenta uniformemente a razón de g' m/s por metro por encima del eje del canal sonoro.
- cm es la velocidad mínima en el eje del canal sonoro.
- La velocidad aumenta uniformemente a razón de g'' m/s por metro por debajo del eje del canal sonoro.
Cuando el gradiente de velocidad g' es constante, los rayos atraviesan el eje del canal sonoro hacia arriba formando un ángulo O1 con la horizontal, por lo que viajarán formando un arco de círculo de radio R' y cruzaran de nuevo el eje del canal sonoro a una distancia horizontal:Por tanto, el rayo atraviesa el eje del canal sonoro en dirección hacia abajo formando un ángulo O2 y cruzará de nuevo a una distancia horizontal:
Generalmente los rayos que atraviesan el eje del canal sonoro formando un ángulo O0, lo volverán a cruzar de nuevo formando este mismo ángulo, primero en una dirección y luego en la contraria.
Vamos a obtener una expresión de la velocidad media horizontal de los rayos acústicos que cruzan el eje de un canal sonoro con un ángulo O0.En el eje del canal sonoro la velocidad del sonido es mínima, es decir c=cm. En cualquier punto del canal sonoro la velocidad de propagación de la onda dada por la ley de Snell:
La componente horizontal de esta velocidad es c.cosO = cx, o sea:
El valor medio de esta velocidad será:
Y desarrollando en serie senO0 y cosO0 nos queda:
donde O0 está en radianes. Por tanto la velocidad media horizontal de los rayos acústicos que atraviesan el eje del canal sonoro es siempre mayor que la velocidad mínima del sonido cm en el eje del canal.