4.    Psicoacústica

La psicoacústica es una rama de la psicofísica que estudia la relación existente entre el estímulo de carácter físico y la respuesta de carácter psicológico que él mismo provoca, es decir, estudia la relación entre las propiedades físicas del sonido y la interpretación que hace de ellas el cerebro.

OBJETIVOS:

Los objetivos generales de la psicoacústica pueden resumirse en determinar:

1.  la característica de respuesta de nuestro sistema auditivo, es decir, cómo se relaciona la magnitud de la sensación producida por el estímulo con la magnitud física del estímulo;

2.  el umbral (absoluto) de la sensación;

3.  el umbral diferencial de determinado parámetro del estímulo (mínima variación y mínima diferencia perceptibles),

4.  la resolución o capacidad de resolución del sistema para separar estímulos simultáneos o la forma en que estímulos simultáneos provocan una sensación compuesta;

5.  la variación en el tiempo de la sensación del estímulo.

Métodos y procedimientos en psicoacústica

La psicoacústica es una disciplina empírica. Los resultados se obtienen estadísticamente a partir de los resultados concretos de los experimentos realizados con cada uno de los sujetos del experimento. Si los resultados son muy dispares, no es posible extraer conclusiones.

Hechos y modelos

La realización de experimentos a efectos de obtener valores y escalas que pudieran reflejar las características del funcionamiento de nuestro sistema auditivo es sólo una parte del trabajo en psicoacústica. La otra componente importante es el diseño de modelos que ayuden a explicar los resultados del experimento, es decir, el funcionamiento del sistema auditivo.

4.1.   Umbrales psicológicos

Dado un tipo de estímulo (como por ejemplo un sonido, una presión sobre la piel o una sustancia agresiva que llega a la sangre), el organismo reacciona con una intensidad que depende, a menudo en forma compleja, de la intensidad del estímulo. En el caso en que el estímulo origina una sensación, es posible medir ésta a través del informe del sujeto, aunque existe el efecto perturbador de la subjetividad, que puede estar influida por diversas  ircunstancias: hábitos, entrenamiento, asociaciones, cultura, etc. En general, el tratamiento de estas reacciones se realiza estadísticamente, sometiendo las variables involucradas a un estricto control. Los resultados suelen ser válidos sólo en determinado contexto sociogeográfico.

Un caso relativamente fácil de medir es el de los umbrales psicológicos. Estos corresponden al mínimo nivel de un determinado estímulo para provocar una reacción observable. Existen dos tipos:

a) Umbrales absolutos

b) Umbrales diferenciales

a) Umbral absoluto: Es la mínima intensidad de un estímulo para la cual en un 50% de los intentos el sujeto considera que el estímulo está presente. Siempre se deben especificar cuidadosamente las condiciones en las cuales se determina el umbral. Por ejemplo, para el umbral absoluto de frecuencia, debe indicarse la intensidad del sonido, si el sujeto se  encuentra en un recinto acústicamente aislado, si está descansado auditivamente, etc. Hay dos métodos para determinar el umbral absoluto:

    1) El de mínimos cambios, que consiste en aproximarse gradualmente desde abajo hasta que el sujeto declara que el estímulo está  presente, y luego desde arriba, bajando hasta que indica que el estímulo desaparece. Se  promedian ambos valores.

    2) El de los estímulos constantes, consistente en exponer al sujeto a estímulos de intensidades fijas alrededor del probable umbral, los cuales se repiten ordenados aleatoriamente. El umbral corresponde al valor que el sujeto declare como presente un 50% de las veces.

b) Umbral diferencial: Es la mínima intensidad con que un estímulo debe exceder a otro para que el sujeto los reconozca como diferentes en un 50% de las pruebas. Al igual que en el caso anterior, son importantes las condiciones de ensayo, entre las cuales debe especificarse la intensidad del estímulo más débil. Para la determinación del umbral  diferencial pueden utilizarse los dos métodos anteriores, o bien el método del error promedio. En éste, el sujeto controla la intensidad del estímulo variable y lo ajusta hasta hacerla "igual" a la de un estímulo fijo. El error promedio cometido es el umbral Diferencial.

Es interesante hacer notar que los umbrales no son valores perfectamente determinados. No sólo los diversos métodos pueden arrojar valores diferentes, sino que además un mismo método puede variar de un momento a otro, ya que el sujeto puede cansarse, o bien agudizar su percepción al realizar más intentos.

4.2.   La ley de Webber Fechner

Esta es una ley empírica que en realidad no se cumple perfectamente, sobre todo fuera del rango central de intensidades de los estímulos. Sin embargo, es indicativa del fenómeno de compresión que caracteriza a la percepción sensorial. Denominando diferencia apenas perceptible (DAP) al umbral diferencial, Weber concluyó, en 1834, que la DAP es proporcional a la intensidad física del estímulo, E,DAP = K·E (2)

o, lo que es lo mismo, que el incremento relativo de intensidad del estímulo correspondiente a una DAP es constante.

Fechner fue aún más lejos, postulando en 1860 que la DAP corresponde subjetivamente a un incremento constante en la sensación provocada por el estímulo. Dicho de otro modo, el incremento en la sensación correspondiente a una DAP puede ser considerado como la unidad de sensación.

Si E es el estímulo y S a la medida de la sensación, buscamos una relación funcional S = f(E) entre ambas que se desprenda de la ley de Weber y el postulado de Fechner. Sean E y E' dos estímulos que difieran en una DAP, es decir

Podemos escribir

Por la ley de Weber,

Asimismo, adoptando como unidad de sensación la provocada por una DAP por el postulado de Fechner,

Se llega así a la ecuación

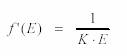
que, integrada, resulta en

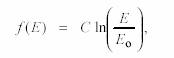
donde C = 1/K, y Eo es un valor de referencia arbitrario (tomado habitualmente como el umbral absoluto). En términos de la sensación:

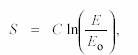
Esta relación logarítmica constituye la ley de Weber Fechner, y como ya se señaló, en general sólo tiene validez en el rango medio de los estímulos.

4.3.   La percepción del tono del sonido

La altura es uno de los parámetros perceptivos fundamentales del sonido. Está íntimamente vinculada a la frecuencia, aunque la afectan un poco la intensidad, la complejidad espectral (cantidad e intensidad relativa de los sonidos parciales), y la duración. Por ello es que al realizar experimentos con la altura es preciso definir cuidadosamente las condiciones en que éstos se efectúan. Existen varias formas posibles de cuantificar la altura.

4.3.1.      Escala tonal a partir del umbral diferencial

La medición más básica de la altura en función de la frecuencia puede realizarse por medio del umbral diferencial, aplicando el postulado de Fechner. El parámetro físico que varía es la frecuencia de un tono puro (senoidal), permaneciendo fija la intensidad.

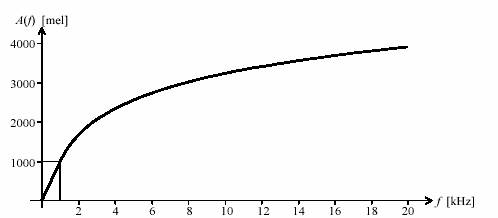
Resulta que hasta los 1000 Hz, la DAP es aproximadamente constante y es del orden de 3 Hz, en tanto que para frecuencias mayores, la DAP es alrededor de un 0,3 % de la frecuencia. Esto implica que la ley de Weber sólo se cumple para las frecuencias mayores de 1000 Hz. Si admitimos el postulado de Fechner, la medida de la altura obtenida a partir de la DAP será lineal para f <1000 Hz y logarítmica para f > 1000 Hz , es decir

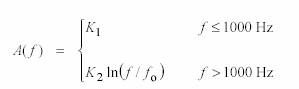
Las constantes se determinan fácilmente si se adopta una escala para la altura. Lo más habitual es tomar como unidad el mel, que se define de modo que para f = 1000 Hz se tenga A(f) = 1000 mel. Resulta

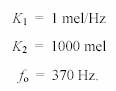
4.3.2.      Escala proporcional de altura

La construcción de una escala de altura a partir del umbral diferencial tiene el inconveniente de que, contrariamente a lo especulado por Fechner, la percepción humana le asigna diferente importancia al umbral diferencial según el valor del estímulo (en este caso, la frecuencia). Una clase completamente diferente de experimentos que permite elaborar otro tipo de escala consiste en tomar un tono de referencia, por ejemplo 1000 Hz, y ajustar la frecuencia de un segundo tono de manera tal que éste parezca el doble de agudo que el otro. Repitiendo el experimento con diversas frecuencias de referencia es posible elaborar una escala de tipo proporcional. La escala obtenida se muestra en la figura 13, en la que también se repite la relación anterior para comparación.

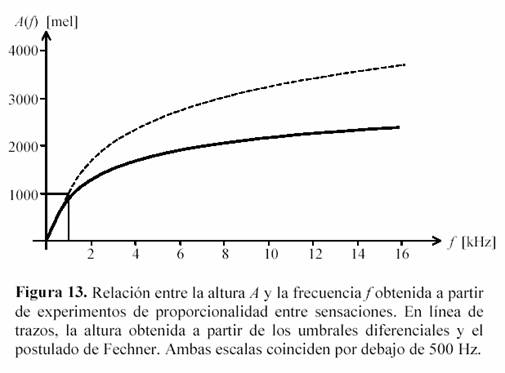
Por debajo de 500 Hz ambas escalas coinciden ya que el crecimiento es lineal. Se observa que para alta frecuencia la escala proporcional ejerce una compresión mayor que la basada en el umbral diferencial, alcanzando un valor de apenas 2400 mel en 16 kHz.

Las dificultades para establecer esta escala experimentalmente son mucho mayores, ya que se requiere de los sujetos un juicio relacional para el que, por añadidura, no disponen de referencias previas asimiladas. La determinación de umbrales diferenciales es más simple pues requiere sólo un juicio binario sobre si se percibe o no alguna diferencia entre dos estímulos.

4.3.3.      La teoría "del lugar"

Si se dibuja en una curva que indica la posición de la máxima amplitud de vibración de la membrana basilar en función de la frecuencia  tomando la distancia desde el ápex en lugar de la base, se obtiene que hay una correspondencia directa entre la representación espectral del sonido y su representación espacial en la cóclea. Es la denominada teoría del lugar,  la cual es parcialmente válida, especialmente para frecuencias superiores a los 1000 Hz.

Esta teoría se inició con Hermann Helmholtz, en el siglo XIX. Helmholtz creía que las células ciliadas ubicadas sobre la membrana basilar (denominadas fibras de Corti) se comportaban como cuerdas, resonando selectivamente con la frecuencia de la misma manera en que lo haría el encordado de un piano sin sus apagadores (o con el pedal derecho oprimido). El mismo Helmholtz encontraba muy difícil de justificar la resonancia para el caso de las frecuencias más bajas, debido a las exiguas dimensiones de dichas fibras. Una comprensión más satisfactoria de la mecánica de la membrana basilar se logró en 1940, con los trabajos de Georg Békésy, quien realizando experimentos sobre cócleas recién extraídas de cadáveres pudo comprobar que era la propia membrana basilar la que se comportaba en forma selectiva, a través de la aparición de “ondas viajeras” como la indicada en la figura 7. No logró, no obstante, explicar la gran agudeza de la discriminación de frecuencias, fenómeno que recién se dilucidaría al descubrirse la contractibilidad de las células ciliadas externas.

4.3.4.      La altura musical o armónica

Las escalas tonales mencionadas anteriormente no tienen en cuenta la incidencia de los aspectos culturales en la valoración de la altura. Una de las principales manifestaciones culturales relacionadas con la altura es la música.

En el caso de la música occidental tradicional, la escala de alturas se rige en realidad por una ley perfectamente Weberiana, como lo es la escala cromática, cuyo mínimo intervalo semánticamente significativo es el semitono, que también se utiliza como unidad. Un semitono equivale a una relación de frecuencias de 2^(1/12)=1,05946.  Así, la altura expresada en semitonos será

Así, si f2 y f1 difieren en un semitono, entonces

Pero

Resulta entonces que

de donde

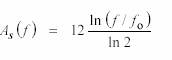
donde fo es la primera frecuencia de la escala. En el caso particular en que f / fo = 2, es decir una octava, resulta As(f) = 12 semitonos. Por eso, una octava de un teclado de un piano tiene 12 teclas:

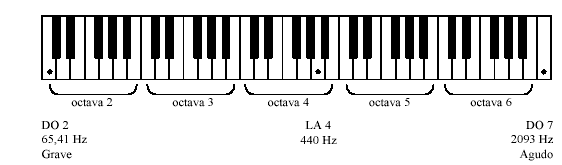
4.3.5.      Superposición de tonos puros

Supongamos que tenemos dos tonos puros de frecuencias angulares w1 y w2 y amplitudes A y B superpuestos. Luego de algunos cálculos, la superposición de ellos es

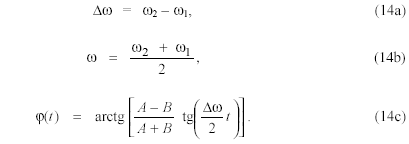
Aparece una modulación de amplitud (AM) y otra de fase (PM). Esta última carece de importancia, dado que el efecto de la modulación de amplitud es siempre mucho más notorio que el de modulación de fase. En el caso en que A = B la superposición se reduce a

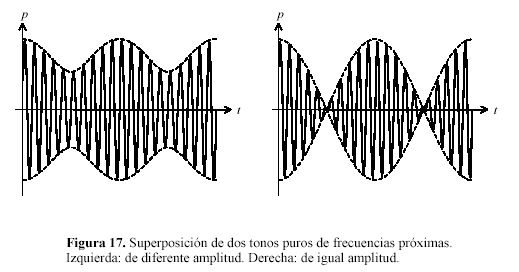
Dado que para pequeñas amplitudes la membrana basilar se comporta linealmente, cuando dos tonos no muy intensos llegan a ella sus efectos pueden superponerse. Dependiendo de la diferencia relativa entre las dos frecuencias hay tres situaciones posibles.

1er CASO: Δw << w1, w2

Como ambos tonos son de frecuencias muy próximas, excitan prácticamente la misma zona de la membrana basilar, sumándose sus efectos. Aparece así un tono de pulsación w parecido a w1 y a w2 modulado en amplitud por una baja frecuencia .Δw, dando origen al fenómeno de batido o pulsaciones, que se percibe como un tono cuya intensidad fluctúa periódicamente entre un mínimo y un máximo.

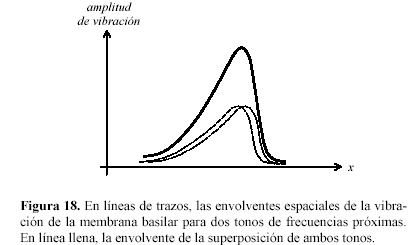
2do CASO: .Δw > Δwd

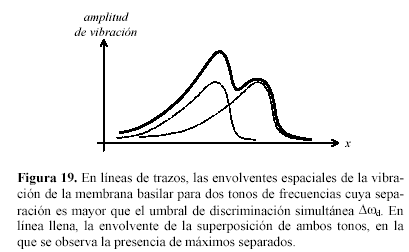
La frecuencia Δwd es el límite de discriminación de frecuencias, por encima del cual se pueden percibir las alturas individuales de ambos sonidos, aunque acompañados de una sensación de agitación o disonancia. Este límite, válido para tonos puros simultáneos, no debe confundirse con el umbral diferencial, que corresponde a una sucesión de sonidos. El límite de discriminación para tonos simultáneos es, normalmente, mucho mayor que el umbral para tonos consecutivos.

En este caso, al sumar las respuestas de la membrana basilar, dado que los máximos correspondientes a cada una de las frecuencias están suficientemente separados, se obtiene una respuesta con dos máximos, evocando cada uno de ellos una sensación de altura diferente (figura 19). Las alturas evocadas son cercanas a las que evocarían los sonidos presentados individualmente, aunque no necesariamente coinciden exactamente con éstas, ya que los máximos aparecen algo desplazados al sumarles una función creciente o decreciente. En la zona intermedia entre ambas frecuencias, la membrana basilar sigue vibrando con amplitud pulsante, aunque con una frecuencia de batido mucho más alta, dando origen a la sensación de agitación o aspereza.

3er CASO: .Δw  >Δwc

Si se sigue aumentando la diferencia de frecuencias entre ambos sonidos, se llega a la frecuencia Δwc, o banda crítica, por encima de la cual desaparece toda sensación de rugosidad, aspereza o agitación, escuchándose los dos sonidos separadamente y sin que interactúen entre sí.

La banda crítica puede considerarse como una especie de ancho de banda que comprende todas aquellas frecuencias que tienen influencia significativa en un determinado punto de la membrana basilar. La existencia de la banda crítica .Δwc es una característica fundamental del oído, que tiene profundas consecuencias sobre su funcionamiento. En particular determina la capacidad de discriminar sonidos en presencia de otros sonidos, así como muchas propiedades psicoacústicas como, por ejemplo, de qué manera se percibe la intensidad de un conjunto de sonidos.

Tanto Δwd como .Δwc dependen en general de la frecuencia, como se indica en la figura 21.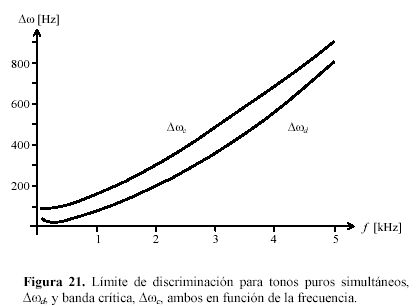

4.3.6.      Fenómenos no lineales en el oído

Hasta ahora habíamos supuesto que tanto en el tímpano como en la cadena de huesecillos, así como en la membrana basilar, valía el principio de superposición, hipótesis que tiene validez sólo para niveles de presión sonora pequeños. Para intensidades sonoras grandes, el sistema mecánico del oído deja de ser lineal y, por consiguiente, al recibir un tono puro (senoidal) de suficiente intensidad, se produce una distorsión caracterizada por la generación de una serie de armónicos. Estos armónicos son audibles, y de hecho existen realmente en la membrana basilar y excitan las correspondientes zonas. En efecto, si la transferencia no lineal entre la entrada x y la salida y es de la forma entonces para x(t)=sen(wt) se tiene que es una función periódica de igual frecuencia que x(t) que, según el teorema de Fourier, posee armónicos, w2,w3, etc. éstos se denominan armónicos aurales, por estar generados en el propio oído. Un caso similar lo constituye la superposición de dos tonos puros e intensos. En este caso, si llegan al oído dos sonidos A1 sen w1t y A2 sen w2t, resulta

Podemos reemplazar f(x) por su desarrollo de Taylor:

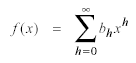
con n, m enteros. Estos tonos se llaman sonidos combinacionales, de los cuales en general el más intenso es el denominado sonido diferencial, de frecuencia | f1­f2|. Este sonido es perfectamente audible, y puede verificarse experimentalmente haciendo sonar dos tonos intensos, uno de frecuencia 1000 Hz y el otro de frecuencia variable, inicialmente de 1000 Hz. Al pasar por 1020 Hz, comienza a percibirse un tono de 20 Hz que va subiendo. Al llegar a 1100 Hz, por ejemplo, el tono escuchado tiene 100 Hz y se percibe con gran nitidez

Los sonidos combinacionales fueron descubiertos por Sorge, organista alemán del siglo XVIII, en 1745, aunque son generalmente atribuidos al violinista italiano Giuseppe Tartini quien los redescubrió en el violín en 1754. Una aplicación interesante es la reconstrucción de la fundamental perdida por insuficiente respuesta en los bajos a partir de los armónicos. Esto sucede, por ejemplo, en las radios portátiles de bajo precio, cuyos parlantes son incapaces de reproducir eficientemente los sonidos de frecuencia inferior a los 100 Hz. Ello implicaría que la voz masculina, por ejemplo, quedaría totalmente distorsionada al faltarle el primer armónico, que se encuentra en esa banda de frecuencia. Pero dado que los armónicos siguientes son reproducidos aceptablemente, están presentes las frecuencias 2f, 3f, 4f, etc., que permiten generar en el oído el armónico fundamental como sonido diferencial entre cualquier par de armónicos consecutivos, por ejemplo

4.3.7.      Fenómenos auditivos a nivel neuronal

Los fenómenos analizados anteriormente se caracterizaban por estimular en la membrana basilar la aparición de ciertas componentes sonoras (tales como los tonos combinacionales) que no estaban incluidas en el sonido original. Existen, sin embargo, diversas situaciones que no pueden atribuirse al comportamiento alineal del oído, dado que la intensidad sonora es pequeña. En estos casos tiene importancia decisiva el procesamiento posterior del sonido a nivel neuronal.

El seguimiento o reconstrucción de la fundamental a partir de los armónicos (descrito anteriormente en conexión con las alinealidades del oído) es un fenómeno cuya explicación completa requiere tener en cuenta los efectos neuronales. En efecto, se trata de una característica del oído que no se circunscribe al caso analizado de sonidos intensos. Un ejemplo de ello es el auricular del teléfono, que reproduce, por limitaciones en la banda de frecuencias del sistema telefónico, sólo las componentes armónicas superiores a los 300 Hz. Esto elimina casi por completo las fundamentales de todas las voces humanas (no se tienen en cuenta en esta afirmación los sonidos más agudos propios del canto). Sin embargo, normalmente las voces no pierden su identidad ni su carácter, aunque difícilmente se pueda considerar que el nivel del auricular telefónico lleve al oído fuera de su rango lineal.

Este fenómeno se apoya en un mecanismo que se relaciona con la capacidad de memorizar los patrones de vibración de la membrana basilar. Sucede que todo ser humano está expuesto desde su nacimiento a sonidos periódicos o quasi periódicos (por ejemplo la propia voz, o la de sus padres). Estos generan arquetipos o patrones de vibración definidos en la membrana basilar cuya audición reiterada induce su aprendizaje. Posteriormente, cada aparición parcial del patrón evoca por asociación el patrón completo. Esto sucede porque la primera reacción del cerebro ante un estímulo nuevo es asociarlo a un patrón ya incorporado a la memoria que difiera poco del patrón correspondiente al nuevo estímulo.

4.4.   La percepción de la sonoridad

La sonoridad es el otro parámetro perceptivo fundamental del sonido. Está vinculada a la intensidad, parámetro físico que describe la energía transmitida por la onda sonora. La sonoridad se ve notablemente afectada por la frecuencia, la duración, etc., de manera que al igual que con otras magnitudes psicológicas, se debe prestar especial atención a las condiciones en que se la determina o especifica.

Antes de proseguir, recordemos que la intensidad sonora se define como la potencia que atraviesa la unidad de área normal a la dirección de propagación de la onda. Para el caso de ondas planas o aproximadamente planas puede expresarse en términos de la presión sonora eficaz de la onda, Pef, como sigue:

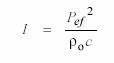
el nivel de presión sonora, definido como

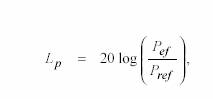
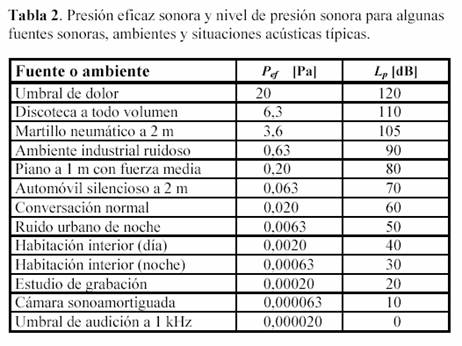
Resulta interesante destacar que una razón frecuentemente aducida para la adopción de una escala logarítmica es el supuesto “comportamiento logarítmico del oído”. Según veremos, la sensación de sonoridad no cumple la ley logarítmica de Weber Fechner, sino una ley potencial con exponente 3/5.

En primer lugar la ley de Weber no es enteramente válida en ningún rango suficientemente amplio de intensidad. Si la intensidad (o la presión sonora) fuera una magnitud Weberiana, la diferencia apenas perceptible sería proporcional a la presión sonora, por lo que el nivel de presión sonora luego de un incremento de una DAP resultaría

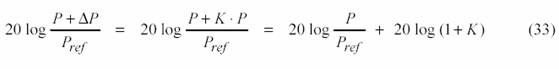
En otras palabras, la diferencia mínima perceptible expresada como nivel de presión sonora debería ser una cantidad constante de decibelios. En realidad la diferencia mínima perceptible se aproxima, para f = 1 kHz, a la curva indicada en la figura 24. Tampoco es válido el postulado de Fechner.

4.4.1.      Umbral de audición

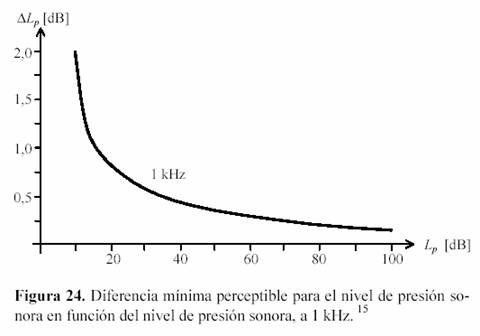
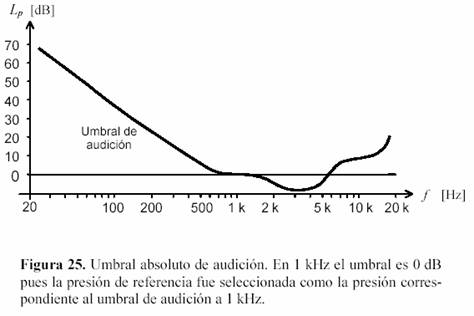
Es el nivel de presión sonora correspondiente al umbral de intensidad. Este umbral depende mucho de la frecuencia, debido a que las distintas partes del oído no son igualmente eficientes para conducir la energía sonora en todas las frecuencias. Así, la resonancia del canal auditivo externo cerca de los 3000 Hz hace que el umbral sea en esa banda de frecuencias mucho menor que a otras frecuencias. El umbral también depende de la persona, y de las condiciones en que se lo determina. Por ejemplo, lo afectan las enfermedades otorrinolaringológicas, la exposición reciente a ruidos y el cansancio. También es común un aumento irreversible del umbral por exposición prolongada (en general, durante varios años) a niveles de presión sonora muy altos, lo cual suele ocurrir en ambientes de trabajo. El aumento del umbral se denomina en general hipoacusia. Finalmente, se observa estadísticamente un aumento del umbral con la edad, conocido como presbiacusia. En la figura 25 se muestra el Lp que corresponde al umbral de audición en función de la frecuencia. La curva representa el valor promedio para personas jóvenes y con el oído en buen estado. Como se puede observar, para 1 kHz el umbral es de 0 dB. Ello se debe precisamente a la forma en que se ha elegido la referencia.

4.4.2.      Curvas de igual sonoridad y nivel de sonoridad

En 1933, Fletcher y Munson realizaron otro tipo de determinación psicoacústica basada en la comparación entre dos tonos puros: un tono de 1 kHz e intensidad fija, utilizado como referencia, y un tono de otra frecuencia e intensidad variable, que el sujeto debía ajustar hasta que fuera igualmente sonoro (o intenso) que el de 1 kHz. Graficando los resultados en función de la frecuencia, obtuvieron para cada intensidad de referencia una curva o contorno de igual sonoridad. Las curvas, denominadas contornos de Fletcher­Munson, se reproducen en la figura 26.

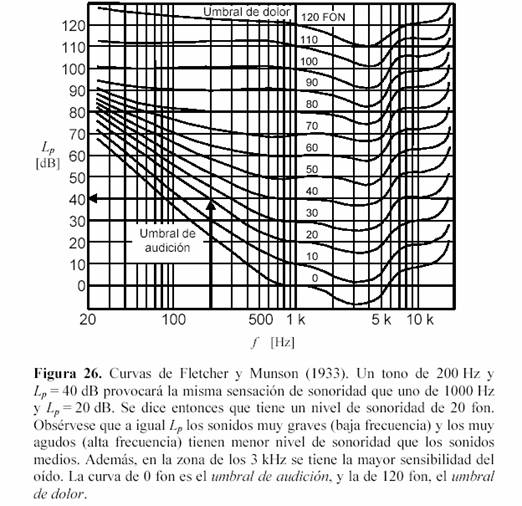
Se han representado allí las curvas de igual nivel de sonoridad cada 10 dB.  Para intensidades elevadas las curvas se van haciendo más planas. Estas curvas permiten comparar la intensidad subjetiva de dos tonos puros de diferentes frecuencias e intensidades. Así, un tono puro de 100 Hz y 50 dB parece menos sonoro que uno de 2 kHz y tan sólo 30 dB. Los menores valores de Lp requeridos en las proximidades de 3 kHz para evocar una misma sensación de sonoridad se deben a la resonancia del canal auditivo en esa frecuencia.

Debe advertirse que estas curvas reflejan en realidad los promedios de un número considerable de personas jóvenes y con el oído en buenas condiciones, pudiendo haber, por consiguiente, variaciones individuales importantes.

Los contornos de igual sonoridad pueden utilizarse para asignar una valoración numérica a la sonoridad. Así, se define el nivel de sonoridad, NS (loudness level, LL), como el nivel de presión sonora del tono de 1 kHz que se encuentra sobre el mismo contorno. Como unidad simbólica se utiliza el fon. Por ejemplo, un tono de 200 Hz y 60 dB está sobre el contorno que contiene al tono de 1 kHz y 51 dB (interpolando), de modo que su NS es de 51 fon.

Sería interesante poder calcular de manera simple el NS de un sonido compuesto a partir de los NS de sus componentes (por ejemplo sumándolos). Lamentablemente, ello no es simple debido a dos causas: el fenómeno de enmascaramiento de un sonido por otro, que hace que el aporte del sonido enmascarado sea insignificante, y el hecho de que el NS, tal como ha sido definido, no provee una escala absoluta que permita determinar cuánto más sonoro es un sonido que otro. Sólo permite dilucidar si es más o menos sonoro. Este problema se enfocará en las secciones que siguen.

4.4.3.      Sonoridad (S)

El nivel de sonoridad analizado es aún una magnitud psicofísica, ya que en última instancia se basa en la comparación de sensaciones con las producidas por una frecuencia (1 kHz) tomada arbitrariamente como referencia. El valor numérico obtenido se refiere a la magnitud del estímulo físico, no a una valoración de la intensidad de la sensación. Así, por ejemplo, un tono de 80 fon no es el doble de sonoro que uno de 40 fon.

A fin de establecer una escala subjetiva de sonoridad se pide a los sujetos que alteren la intensidad de un sonido en una proporción determinada, por ejemplo hasta lograr un sonido 2 veces más sonoro que el original. Para este tipo de experimento es necesario que los sujetos atribuyan un significado inequívoco al concepto de duplicación de la sonoridad. Esto puede lograrse por comparación entre la audición monoaural y biaural de un mismo sonido. Un sonido B escuchado monoauralmente es doblemente sonoro que otro A cuando produce el mismo incremento de sensación que produce pasar de la escucha monoaural a la escucha biaural de A.

El experimento se realiza con varios niveles de presión sonora, cubriendo todo el rango audible y con una cantidad suficientemente numerosa de sujetos. Luego se procesan estadísticamente los resultados. El resultado es una relación entre el nivel de sonoridad expresado en fon y la sensación de sonoridad, o simplemente sonoridad, S (loudness, L). Expresando la sonoridad en son, unidad que corresponde a un nivel de sonoridad de 40 fon, se obtiene la función de transferencia indicada en la figura 28.

A partir de un nivel de sonoridad de 40 fon la relación es exponencial, ya que, según se aprecia,

de donde

Esta relación es válida sólo para NS > 40 fon, pero como 40 fon representa un nivel de sonoridad bastante bajo (corresponde al ruido ambiente diurno en una habitación de un barrio tranquilo), en la práctica es aplicable a la mayor parte de los sonidos habituales.

Si bien la relación entre el nivel de sonoridad y la sonoridad fue obtenida para tonos de 1 kHz, es aplicable con independencia de la frecuencia, debido a que para otras frecuencias pueden aplicarse previamente los contornos de igual sonoridad.

Para el caso de un tono de referencia de 1 kHz, podemos obtener una conclusión interesante. Recordemos que para el tono de referencia el nivel de sonoridad en fon coincide numéricamente con el nivel de presión sonora:

Entonces

expresión válida para Lp > 40 dB y 1 kHz.

Resulta así que la sensación de intensidad, expresada a través de la sonoridad, dista mucho de cumplir con la ley de Weber Fechner, ya que no se vincula logarítmicamente sino potencialmente con la magnitud del estímulo físico (ya sea que éste se represente con la presión o con la intensidad sonora). Si bien esta conclusión fue obtenida para 1 kHz, es válida para otras frecuencias con pequeñas modificaciones.

4.4.4.      Sonoridad para sonidos compuestos

En la sección anterior se estudió la relación entre el nivel de presión sonora y la sonoridad para el caso de los tonos puros. La mayoría de los sonidos que se encuentran en la práctica no son, sin embargo, tonos puros, sino que están formados por una gran cantidad de componentes armónicos superpuestos.

La extensión del concepto de sonoridad a estos sonidos no es sencilla ni obvia, ya que los mecanismos de integración de la sensación difieren según la separación entre las frecuencias de los componentes, evaluada en términos de las bandas críticas.

Si los sonidos puros que forman el sonido compuesto están comprendidos dentro de una misma banda crítica, la intensidad (o lo que es equivalente, el cuadrado de la presión sonora) total se obtiene sumando las intensidades individuales. A partir de la intensidad, por aplicación de las curvas de igual sonoridad y luego la función de transferencia, puede obtenerse la sonoridad correspondiente a dicha banda crítica.

Si, en cambio, los tonos puros están suficientemente alejados, vale decir a más de una banda crítica entre sí, la sonoridad total se obtiene directamente sumando las sonoridades individuales.

El procedimiento práctico para calcular el nivel de sonoridad consiste en subdividir el espectro del sonido compuesto en bandas críticas, luego sumar las intensidades dentro de cada banda, convertir la intensidad en nivel de sonoridad y éste en sonoridad, y finalmente sumar todas las sonoridades de las diversas bandas críticas y convertir en nivel de sonoridad. Para la aplicación de este método se pueden utilizar los valores de la tabla 4.

Ejemplo 1: Calcular la sonoridad de una onda cuadrada de 200 Hz y nivel de presión

sonora Lp = 60 dB.

En la onda cuadrada los armónicos son de orden impar, y sus amplitudes están en relación inversa con el orden correspondiente. Calculemos primero el Lp de los primeros armónicos. Si la presión eficaz es P, dado que el valor eficaz de una onda cuadrada coincide con su amplitud, los armónicos tienen una amplitud de 4P/P, 4P/3P, 4P/5P, etc, y sus valores eficaces se obtienen dividiendo por 2 . Así, los niveles de presión sonora resultan:

y así sucesivamente. En la tabla 5 se indica el ancho de las bandas críticas y se convierten los Lp a NS y luego a S, utilizando sucesivamente las curvas de igual sonoridad y la función de transferencia. El cálculo se efectuó por computadora.

Como se puede observar, dado que los armónicos están equiespaciados y en cambio las bandas críticas van creciendo, a partir de la banda crítica centrada en 4000 Hz entran varios armónicos en cada banda. Con el valor final en son puede obtenerse

Este nivel de sonoridad es mucho mayor que lo que haría suponer el NPS de 60 dB, lo cual se debe a la gran cantidad de armónicos de alta frecuencia que contiene la onda cuadrada.