Las técnicas de procesamiento de audio tanto en tiempo como en frecuencia se realizan sobre la señal sonora muestreada x[n] puesto que es mucho más sencillo tratar una señal digital que una analógica. El procesado de la señal discreta se suele llevar a cabo con circuitos específicos para tal fin, como son los DSP (Digital Signal Proccesor) que poseen los elementos necesarios para tal fin. Los efectos de tiempo se basan en modificar los intervalos temporales de la reproducción de las muestras, dependiendo del método en concreto se consigue un efecto u otro. Se van a detallar tres efectos ampliamente usados en el procesamiento de audio comercial: Delay, Chorus y Phaser.
Delay
Una de las técnicas más comunes en el procesado de audio digital , y que es base para otras posteriores es el delay o retraso. Básicamente se trata de retrasar las muestras de la señal a modificar, matemáticamente si x[n] es la señal de audio discretizada,
y[n]=x[n-N].
Un retraso de la señal no crea en principio ningún efecto especial sobre el oyente, pero una superposición o suma de señales retrasadas cada una con un retraso diferente puedo ser suficiente para simular fenómenos acústicos como el eco, la reverberación, u otros aspectos de la psicoacústica explicados anteriormente.
En función del retardo aplicado, se puede generar un efecto u otro, por ejemplo se sabe que si dos estímulos sonoros llegan al oído separados más de 50 ms, el cerebro perfectamente distingue los dos estímulos y los "reproduce" sucesivamente en el tiempo. Si la distancia temporal es menor se captarán los dos estímulos como uno solo pero más continuado en el tiempo, dando una sensación de espacialidad.
Para realizar diferentes retardos de la señal de audio original lo que se realiza es una estructura como en la figura 23. La señal x[n] se retarda además de multiplicarse por un determinado valor, diferente en cada caso, para posteriormente sumarse. Es lo que se conoce como el delay multi-tap:
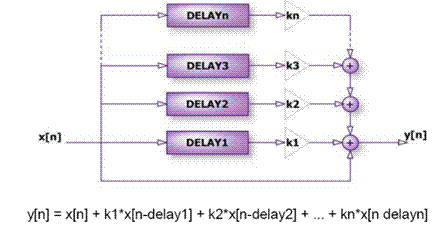
Figura 25. Delay Multi-Tap. Imagen tomada de [3] |
La señal de salida y[n] es :
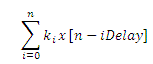
Estamos ante un Filtro FIR (Finite Impulse Response) donde la respuesta al impulso h[n] esta formada por la sucesión de coeficientes anteriores.
En definitiva, aunque el delay se trata de un tratamiento relacionado con el tiempo, al variar los coeficientes varía h[n] y por su puesto su transformada de Fourier Discreta (DFT) que
indica el comportamiento frecuencial de la señal de audio. Las técnicas en tiempo no son independientes del comportamiento en frecuencia.
El efecto generado con un muli-tap Delay se puede escuchar en el siguiente enlace donde se repite una frase sin aplicar el efecto y posteriormente aplicándolo.
Escuchar (Formato WAV - Sonido 3 Tomado de [11])
El efecto es bastante notable, se puede apreciar una sensación de eco poco agradable, seguramente los retardos aplicados sean mayores de 50 ms.
En cambio en el siguiente se consigue un sonido más perfeccionado y más agradable.
Escuchar (Formato WAV - Sonido 4 Tomado de [11])
Si el retardo es suficientemente pequeño, menor de 50 ms se consigue un efecto que da sensación de un sonido continuado, gracias al efecto Haas.
Si el retardo es mayor de 50 ms, este sistema podría simular el efecto de eco en un zona donde se produzcan tantas reflexiones como líneas de retardo haya, similar al primer enlace de audio
Además para mejorar la calidad de sonido, se puede pensar en una reproducción del sonido por dos canales, canal izquierdo y canal derecho, (Sonido en estéreo), y un delay diferente para cada canal para generar una determinada sensación, esa estructura se llama
delay Ping-Pong:
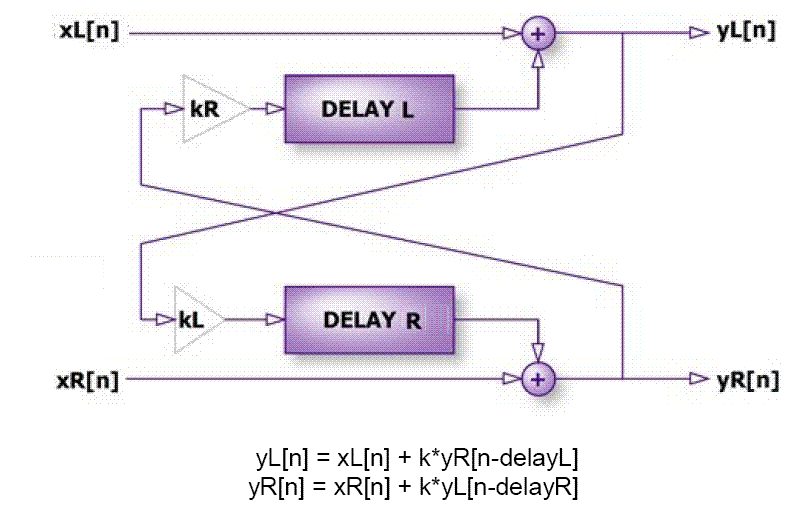
Figura 26. Delay Ping-Pong. Imagen tomada de [3] |
Con esta configuración se consigue un efecto bastante interesante, pues como se aprecia en la Figura por el canal izquierdo sale lo que se pensaba reproducir por ese canal más lo que se reprodujo por el canal derecho unos intantes antes. Con el canal derecho ocurre lo mismo.
Chorus
El efecto Chorus trata de simular el efecto de un Coro (Chorus en Inglés). En un coro musical los miembros intentan cantar lo mismo a la vez pero debido a que esto es imposible, siempre existirá un retardo de cada miembro respecto a otro. Esto que surge por la imprecisión humana se puede generar digitalmente con una serie de delays , pero en este caso variables, una muestra se suma con la misma muestra n posiciones atrás, otra muestra lo hará con otra que estaba m posiciones atrás, etc. Los valores m y n en principio son diferentes y vienen determinados por el delay variable generado. Para recrear la imperfección del coro los delays deben ser indepedientes unos de otros, deben ser aleatorios en la mayor medida de lo posible. Como esto técnicamente es complicado una forma de realizar delays pseudo-aleatorios es usar un oscilador de baja frecuencia (LFO),
donde el voltaje que este genera indica el incremento de delay que se le añade a un delay fijo para crear uno totalmente variable.
Para que no se produzca una sensación de eco el delay variable siempre debe ser menor que 30ms. El delay fijo se puede fijar a 20ms y se deja que las variaciones de delay estén entre 0 y 10ms.
Gráficamente:
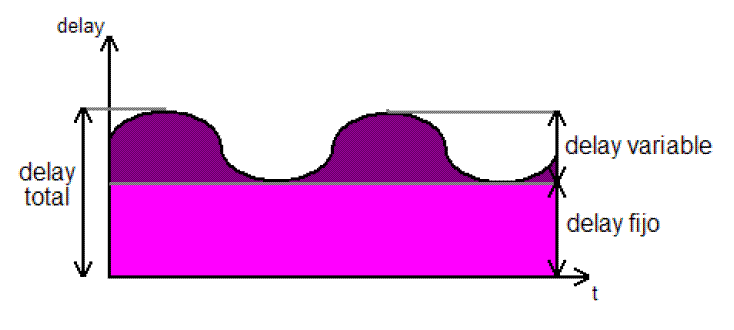
Figura 27. Delay Variable. Imagen tomada de [3] |
Para entenderlo mejor, en un instante temporal digamos to, el delay aplicado es el delay fijo + el delay variable donde este último es el voltaje que tiene la onda en el instante to. Cuando haya que añadir un delay nuevo, por ejemplo en el instante t1, el delay aplicado será delay fijo + delay variable, es decir delay fijo + V(t1).
Si la frecuencia es muy alta se cambia de delay muy rápidamente por eso se usa un oscilador de baja frecuencia , normalmente de frecuencias menores a 3hZ.
La onda del oscilador puede ser de la forma que se desee, en la figura anterior se ha supuesto una onda sinusoidal, pero se puede pensar en ondas diferentes, siempre periódicas, por ejemplo en forma logarítmica o rampa.
Al ser la función logaritmo una que crece bastante despacio usar un oscilador logaritmo hace que el delay aplicado no cambie muy bruscamente:
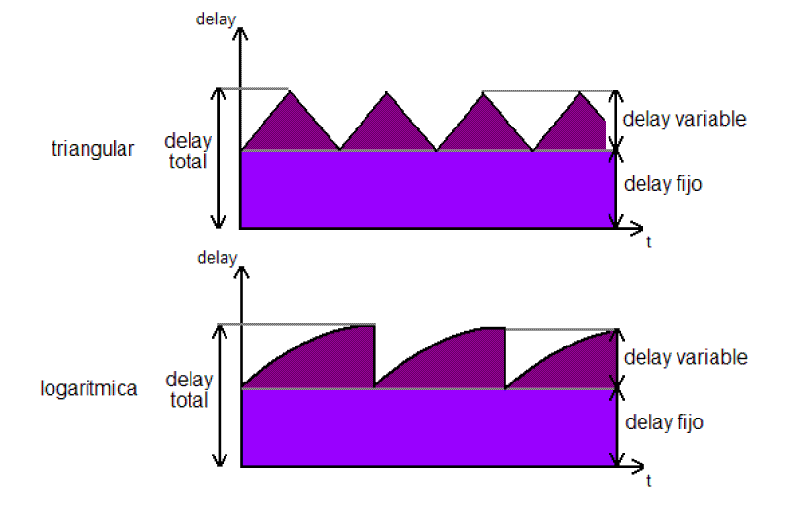
Figura 28. Formas de Onda. Imagen tomada de [3] |
Otra forma de generar un delay variable sin hacer que este sea el voltaje del LFO en un instante determinado es suponiendo que el delay variable es
(Limite/2 )*(1+V(t))
Gracias a esto podemos controlar el máximo del delay variable que como se comentó antes debía ser 10ms. Si la onda del oscilador (V(t)) varía entre -1 y 1, fijando Limite = 20 ms, delay variable oscila entre 0 y 10 ms y por tanto
el delay total varía entre 20 y 30 ms.
Un LFO, no es más que un circuito amplificador, pudiera ser un amplificador operacional como el ua741 explicado en la sección anterior pero es má común que sea un circuito con algun transistor BJT que cumpla los requisitos para que al cerrar la realimentación genere una onda
sinusoidal. La frecuencia de la onda oscilante esta fijada por los elementos usados, ciertos condensadores y ciertas resistencias.
Por ejemplo, el siguiente circuito oscila a una determinada frecuencia fijada por los valores de R1, R2, C1 y C3. La realimentación se realiza a través de C2. En este caso la frecuencia de LFO es de 7.86 Hz, un poco grande para actuar como delay variable en un chorus.
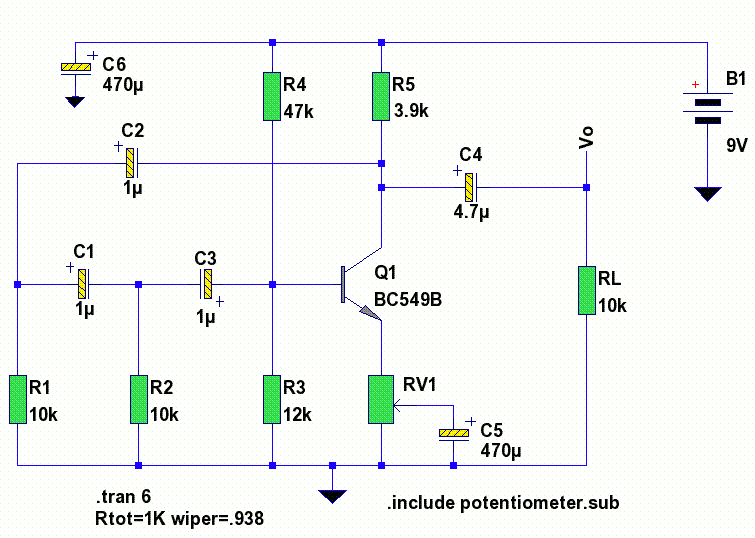
Figura 29. Estructura de un LFO. Imagen tomada de http://www.zen22142.zen.co.uk/Circuits/Testgear/lf_osc.htm |
La etapa más sencilla utilizado un chorus es la siguiente:
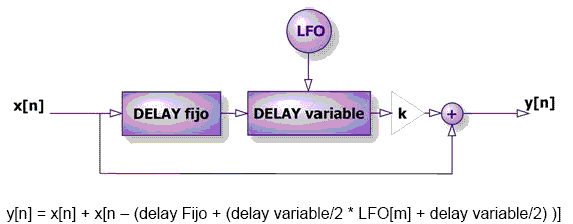
Figura 30. Estructura para generar un Chorus simple. Imagen tomada de [3] |
Con esta estructura se simula un coro con dos fuentes sonoras, pudieran ser dos instrumentos o dos cantantes. Para simular un coro más grande simplemente se repite esta estructura n veces con n osciladores de baja frecuencia, creando un Chorus - Multitap:
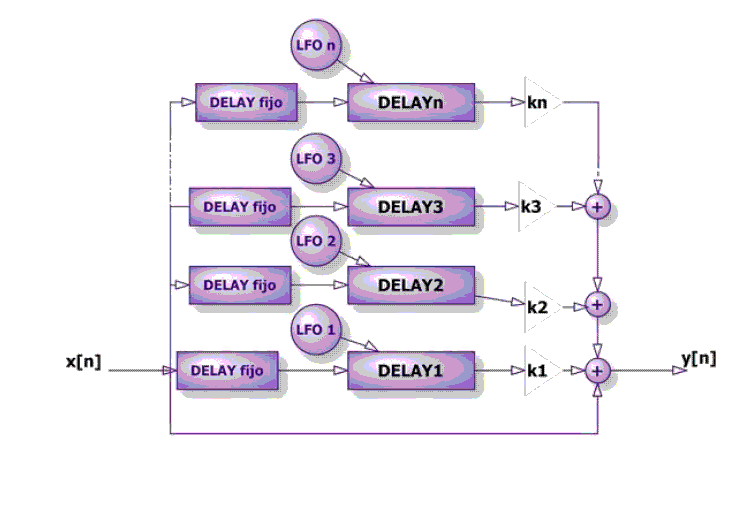
Figura 31. Chorus Multi-Tap. Imagen tomada de [3] |
Otra opción es usar una realimentación (feedback) con la señal de salida:
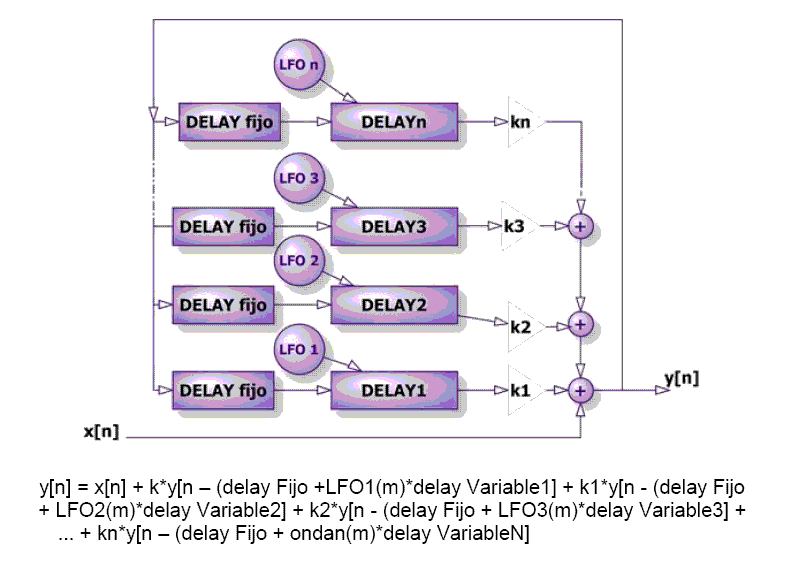
Figura 32. Chorus Multi-Tap con realimentación. Imagen tomada de [3] |
Con esta estructura teóricamente las muestras estarán sonando continuamente, ya que realmente estamos ante un filtro IIR (Infinite Impulse Response) por lo que hay que asegurar su estabilidad, fijando un valor bajo para el depth,parámetro que determina si el sistema se vuelve estable o inestable.
Flanger
El flanger utiliza de nuevo la técnica del delay variable, similar al chorus aunque se utilizan unos valores inferiores a éste último, normalmente delays variables menores de 10 ms. La implementación de este efecto es retrasar cada muestra de la señal de audio un delay variable, que puede hacerse de forma aleatoria o determinista (se puede controlar el retardo para generar diferencias ambiente musicales) y sumarse finalmente.
En la figura de abajo , se representa esquemáticamente este proceso:
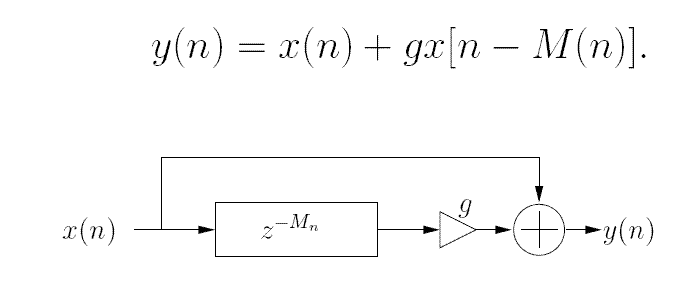
Figura 33. Esquema básico del Flanger. Imagen tomada de [10] |
Si en un instante se está reproduciendo la muestra n-ésima, a esta muestra se le sumará (teniendo en cuenta el factor g) la muestra que se reprodujo M(n) muestras atrás. Como se ve M(n) cambia con la muestra, por lo que al salir la muestra 500 , esta se puede sumar con la muestra 500-30, pero la muestra 600 lo puede hacer con la muestra 600-74 por ejemplo.
La forma de generar el delay variable es la misma que con el chorus , utilizando un LFO que fije los límites de dicho delay y determine el valor de M(n).
Estructura para generar un flanger, como se aprecia es muy similar a un chorus.
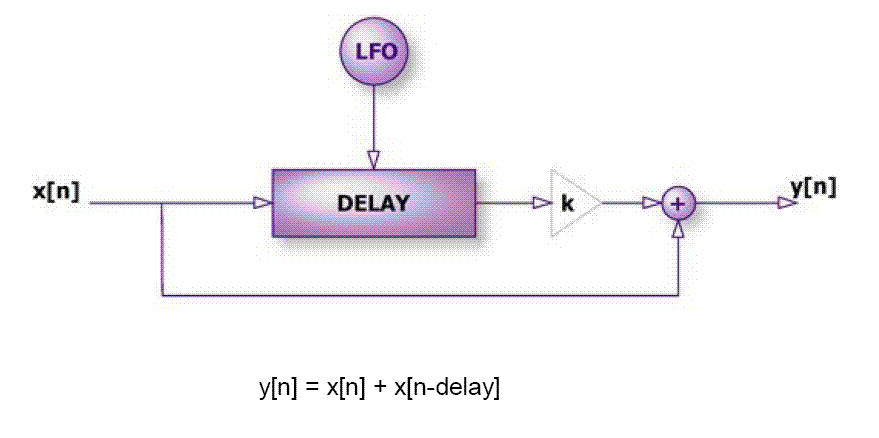
Figura 34. Estructura para implementación del Flanger. Imagen tomada de [3] |
El flanger es el ejemplo más claro de que un efecto técnico en tiempo tiene una gran repercusión en el espectro de frecuencia. Para entenderlo, supongamos el caso de un tono simple, de frecuencia w. Si se retrasa esa señal un valor (T) tal que wT=pi radianes, se tiene la señal anterior pero de signo opuesto y por tanto al sumarse se anulan. La componente frecuencial que existía en la pulsación w ( Una delta) desaparece.
El análisis de Fourier demuestra que si una función cumple una serie de requisitos se puede expresar como una serie infinita de funciones sinuosidales cada una de frecuencia distinta.
En la práctica en la mayoría de los casos una señal de audio se puede recrear o aproximar por una serie finita de tonos sinusoidales. Al aplicarle un retardo variable a la señal en un instante determinado , se cancelan algunos tonos, en otro instante otros y por ello sus componentes frecuenciales se eliminan, se crean lo que se conoce
como notches. La respuesta frecuencial del sistema se conoce como comb filter (Filtro de Peine).
Si los delays son grandes se eliminarán componentes frecuenciales bajas , si son pequeños ocurrirá lo contrario.
Las posibilidades de recrear diferentes ambientes son muy amplias, pues se puede llevar a cabo un control de la atenuación aplicada a los notches, en función del parámetro DEPTH.
A continuación se muestra los diferentes espectros de frecuencia en función del valor del DEPTH, comprendido entre 0 y 1:

Figura 35. Espectro Frecuencial en función del DEPTH. Imagen tomada de [10] |
Otra forma de justificar la forma de la gráfica de arriba es analizando la respuesta en frecuencia de este sistema.
Para ello, supongamos que en un instante temporal discreto n, la relación salida entrada es la siguente (igual que en la primera figura):
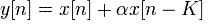
Donde el parámetro alfa se corresponde con el DEPTH del sistema. Aplicando la Transformada Z a ambos lados de la ecuación se obtiene que la
función de transferencia es:
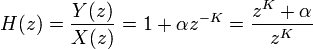
Para obtener la Transforma de Fourier, se evalua la función anterior en puntos de la forma z=exp(jw), y utilizando la Identidad de Euler se llega a que :
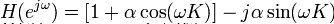
Como lo característico del Flanger es la respuesta en módulo, este es:
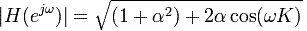
La atenuación total de una componente frecuencial se produce únicamente si alfa es igual 1, y wK es un múltiplo impar de pi.
Ya que de esta forma el coseno de wk es -1 y la expresión de dentro de la raíz es (1-alfa) al cuadrado, que evidentemente cuando alfa es igual 1 es 0.
En el siguiente enlace se puede escuchar el efecto Flanger.
Escuchar (Formato WAV - Sonido 5 Tomado de [11])