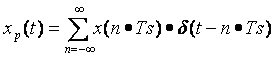
Ahora que ya conocemos las bondades del mundo digital veremos cómo conseguir una señal digital a partir de una analógica. Los pasos que se han de seguir para ello son, en este orden, el muestreo, la cuantificación y la codificación.
El muestreo consiste en obtener muestras equiespaciadas temporalmente de la señal analógica. Esto es, almacenamos el valor de la señal de entrada cada Ts segundos, siendo Ts el periodo de muestreo y fs=1/Ts la frecuencia de muestro(el número de muestras por segundo que se toman), matemáticamente este proceso puede representarse como sigue
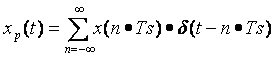
Esta señal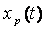
tomará el valor que tome la señal en los instantes 
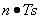y cero en el resto. Posteriormente se pasará la señal por un conversor continuo/discreto que convierta esas deltas continuas en deltas discretas.
Es evidente que la señal muestreada no será igual que la analógica de entrada, pues no estará definida en todos los instantes de tiempo. Por lo tanto, surge la pregunta de si será posible volver a obtener la señal inicial a partir de la muestreada. Para responder a esto hemos de ver 2 parámetros: La frecuencia de muestreo, fs, y la máxima frecuencia de la señal analógica, que se relacionan mediante el Teorema de Nyquist-Shanon.
Antes de describir esto, veamos como varía la señal muestreada (sen(2*pi*5*t) con una fs muy baja(20Hz) (izquierda) y una fs alta (100) (derecha):
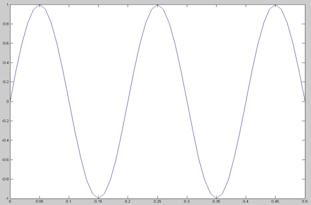
Como se ve, en el primer caso la señal muestreada no es capaz de seguir la variación de la señal de entrada. En ambos casos no tenemos todas las muestras de la señal(pues son infinitas) si no solo un conjunto discreto de ellas luego, ¿Por qué en el segundo caso obtenemos una señal igual a la de entrada y el primer caso no? La respuesta la da el Teorema de Nyquist-Shanon:
Sea x(t) una señal de banda limitada con X(jw)=0 para |w|> . Entonces x(t) se determina unívocamente mediante sus muestras con n=...-3,-2,-1,0,+1,+2,+3,+4...si
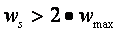
Donde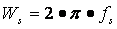 
y 
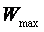es la máxima frecuencia de la señal analógica.
Por lo tanto, la frecuencia de muestreo habrá de ser mayor que 2 veces la frecuencia máxima de la señal analógica y además, cuanto más alta sea fs, mejor. Sin embargo, a mayor fs tendrémos más muestras y por tanto un bitrate mayor. Hemos de encontrar una solución óptima de compromiso entre una fs y un bitrate óptimos.
Para entender todo esto hablemos de la caracterización frecuencial de las señales, haciendo uso para ello de la transformada de Fourier:
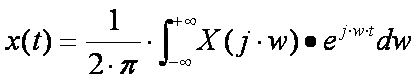donde
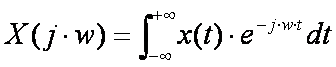
Esta X(jw) representa la distribución en frecuencias de la señal x(t), por ejemplo, si calculamos X(jw) de la función sen(2*pi*100*t) esperaremos obtener componentes frecuenciales en 100Hz y -100 Hz:
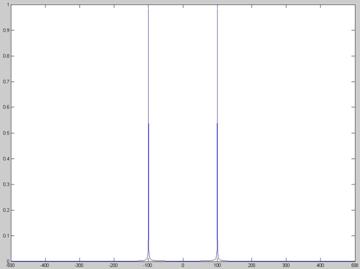
Ahora que ya sabemos que X(jw) representa el espectro frecuencial de x(t), pasemos a ver las implicaciones que el proceso de muestreo tiene en este espectro:
Recordando que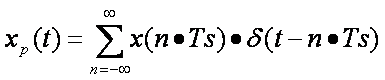 
, que multiplicar en el tiempo es convolucionar en frecuencia y que
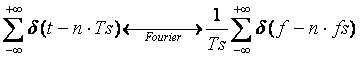
Se verifica que:
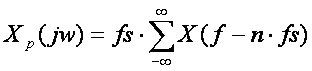
Es decir, el espectro de la señal muestreada es igual al de la de entrada pero escalado por y repetido en múltiplos de . Es decir, si el espectro de nuestra señal de entrada es:
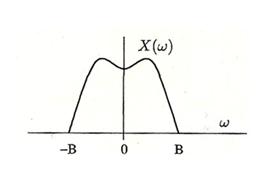
El espectro de la señal muestreada será:
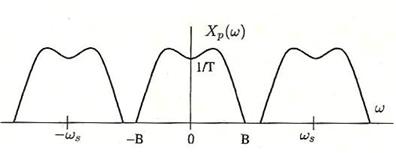
A partir de estas 2 figuaras podemos entender perfectamente el Teorema de Nyquist Shanonn. Si , siendo B la frecuencia máxima de la señal, podremos filtrar pasobajo y quedarnos solo con el espectro pasobajo, obteniendo así la señal original. En cambio, si no se cumple que tendremos solapamiento entre espectros y no podremos obtener la señal original de ninguna manera.
Ahora ya tenemos una señal discreta en tiempo: El siguiente paso será discretizar en amplitud, este paso es conocido como cuantificacion. Este proceso consite en asignar los infinitos valores de amplitud de la señal de entrada en un conjunto finito de amplitudes. La siguiente figura ilustra bien el proceso:
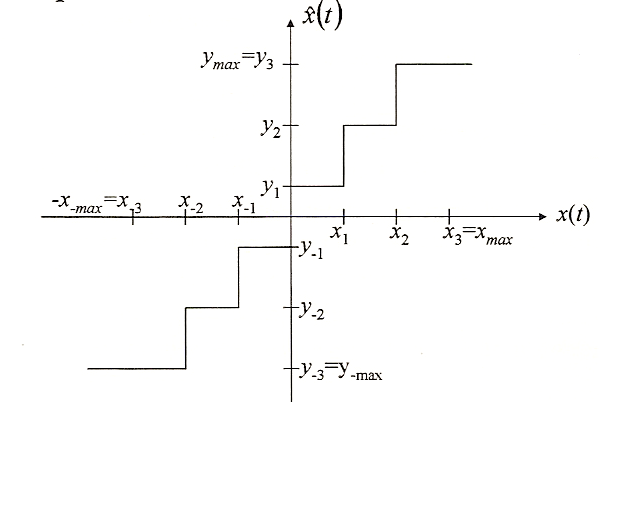
Si la amplitud de entrada se encuentra entre 0 y x1 se le asigna un valor de amplitud de salida de y1; Si está entre x1 y x2, el valor de salida será de y2 y así sucesivamente. Es decir, se transforma un intervalo de amplitudes por un único valor de amplitud, que normalmente coincide con el punto medio de ese intervalo. En total tenemos N= 6 niveles de cuantificación (se necesitarían 3 bits).
La cuantificación es un proceso necesario, pues un sistema digital no puede procesar una señal con infinitos posibles valores. Sin embargo, conlleva inherentemente 2 problemas:
En función del número de bits que utilicemos para codificar cada muestra tendremos más o menos niveles de cuantificación.
Sean n=número de bit por muestra; L= Número de niveles del cuantificador; q=Altura del escalón y Vpp= Voltios pico a pico de la señal de entrada.
se verifica 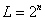que 
y que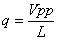 
Además, un parámetro que mide la calidad del cuantificador es la relación señal a ruido de cuantificación (SNRq), que vendrá dada por:
Otro parámetro importe del cuantificador es el Margen dinámico, que se define como la diferencia ente el valor máximo y mínimo que admite el cuantificador.
Es evidente que a mayor número de bits por muestra mayor número de escalones tendremos y mayor se parecerá la señal cuantificada a la original. Por desgracia, incrementar el número de bits por muestra también incrementa, en la misma proporción, el bitrate de la señal. Luego estamos en un compromiso entre aumento de la calidad de la señal y del bitrate.
A modo de ejemplo, se cuantifica una señal sinusoidal, donde la señal cuantificada solo puede tomar los valores [-0.9 -0.7 -0.5 -0.3 -0.1 0.1 0.3 0.5 0.7 0.9]:
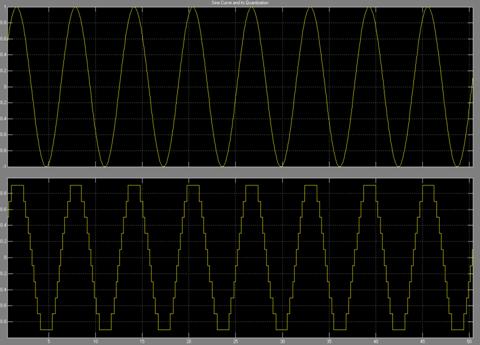
Es importante destacar que el cuantificador ha de estar adaptado a la señal de entrada, es decir, ambos han de tener el mismo rango dinámico y, además, cuanto más rápido varíe la señal de entrada más escalones de cuantificación necesitaremos para obtener una calidad aceptable. Por ejemplo, si la señal de entrada varía entre -5 y 5 Voltios y usamos un cuantificador cuyo margen dinámico esté entre -10 y 10 Voltios estaremos desaprovechando la mitad de los niveles de cuantificación. Al contrario, si para la misma señal usamos un cuantificador de margen dinámico entre -2 y 2 Voltios los valores superiores a 2 voltios (o inferiores a -2 Voltios) no seremos capaces de cuantificarlos.
Hay que destacar que 2 señales cuyo margen dinámico sea el mismo y que varíen con la misma frecuencia no tienen por qué repartirse igualmente en amplitud. Es decir, una puede repartirse más por niveles de amplitud bajos y otra por los altos. Esto es lo que ocurre habitualmente con las señales de voz, que se reparten mucho más por los niveles bajos de amplitud. Debido a esto es evidente que usar una cuantificación uniforme (esto es, que todos los escalones de cuantificación tenga la misma anchura) no es eficiente, pues si la señal se reparte más por los niveles bajos de amplitud será preferible asignar escalones más pequeños a estas amplitudes y escalones más anchos para amplitudes más altas( y, por lo tanto, menos frecuentes en el caso de la voz).
La función de transferencia de los cuantificadores no uniformes sería como sigue:
Donde se ve que los escalones con amplitud de entrada pequeña (x(t) pequeña) son más estrechos que los de amplitud de entrada grande(x(t) grande).
Desgraciadamente no existen comercialmente cuantificadores no uniformes por lo que el camino para llevar a cabo esto habrá de ser aplicar una transformación sobre la señal de entrada, cuantificar uniformemente de la forma habitual y aplicar otra transformación (inversa a la transformación inicial) a la señal cuantificada.
La transformación inicial recibe el nombre de compresión y tiene como objetivo expandir los niveles de amplitud de señal bajos y comprimir los altos. Al hacer esto lo que se consigue es que la señal se reparta en amplitud de forma más o menos uniforme.
A continuación se cuantifica uniformemente y, gracias a esa transformación inicial, ahora ya si será eficiente cuantificar de esta forma.
Finalmente se lleva a cabo sobre la señal otra transformación, denominada expansión, que tiene como objetivo hacer que la señal se reparta en amplitud tal y como lo hacía antes de la compresión. Así se devuelve la señal a su forma original(pero cuantificada).
El proceso se puede resumir en:
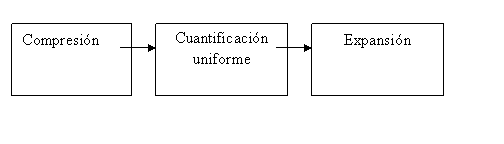
Para llevar a cabo las 2 transformaciones anteriores (compresión y expansión) se hace uso de dos leyes: La ley A y la Ley µ
La ley A es un estándar europeo(que se usa para el códec G.711 para telefonía) y la formula de transformación es como sigue:
.
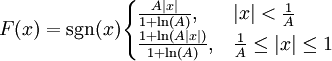Donde “x” sería la amplitud de entrada normalizada, es decir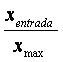 
y F(x) sería la amplitud de la señal tras la transformación. Como se ve, esta función es lineal en el primer tramo
y logarítmica en el segundo.Estos tramos están delimitados por el valor de A. Típicamente A=87.6 y,
a mayor valor de A se aumenta el tramo no lineal. Para un valor de A=0 no existe compresión pues, si A=1, se tiene:
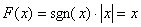para |x|<1
La función de expansión sería la inversa de la de compresión es decir, se obtendría sin más que despejar x de la ecuación anterior:
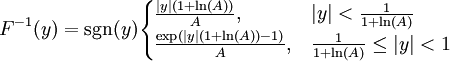
Donde y sería la amplitud de entrada al expansor (normalizada por su valor máximo) y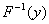 
el valor de salida del cuantificador completo.
Para ver como afecta está función de transformación se puede acudir a la siguiente gráfica:
Donde se aprecia que para A=1 (la curva es una recta de pendiente=1) la función no realiza transformación alguna. Además puede verse que a mayor A más se rápido crece la gráfica inicialmente para amplitu des de entrada bajas y más lento para amplitudes de entrada altas. Por lo tanto, a mayor A tendremos escalones de cuantificación correspondientes a amplitudes bajas cada vez más estrechos.
Mientras la ley A se utiliza principalmente en Europa, existe también una ley con el mismo fin y caracteristicas similares conocida como Ley µ que se utiliza en países como Estados Unidos, Canadá o Japón.
Sus ecuación de tranformación es como sigue:
Donde x es la amplitud de entrada normalizada por su valor máximo y µ es un parámetro que típicamente toma el valor de 255. Si µ=0 se tiene que no existe compresión:
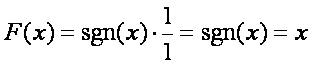
La función de expansión sería la inversa de la de compresión y se obtendría sin más que despejar x.
Para ver como afecta está función de transformación (con Ley µ) se puede acudir a la siguiente gráfica:
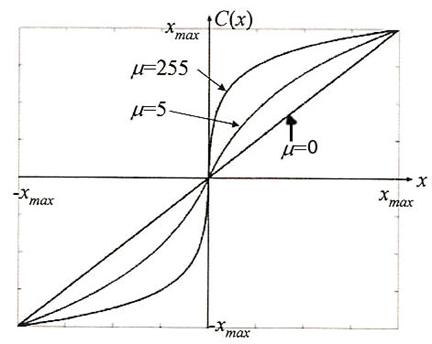
Donde se aprecia que para µ=0 (la curva es una recta de pendiente=1)no se realiza transformación alguna sobre la señal y que, a medida que aumenta los niveles de amplitud bajos se expanden y los de amplitud alta se contraen.
Pasemos a ver ahora de forma gráfica los efectos de estas transformaciones y veremos que la cuantifiación no uniforme no siempre es más efectiva que la uniforme:
La señal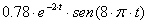 
es una señal que se reparte mucho más por los niveles bajos de amplitud que por los altos, con lo cual puede ser útil para ver las bondades de las leyes A y µ:
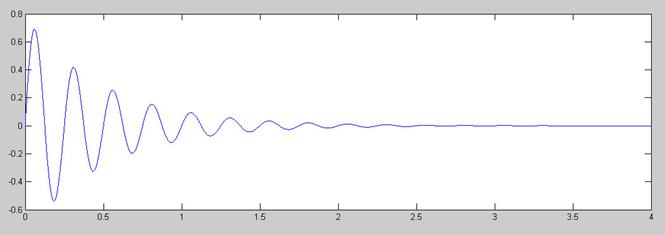
Señal original
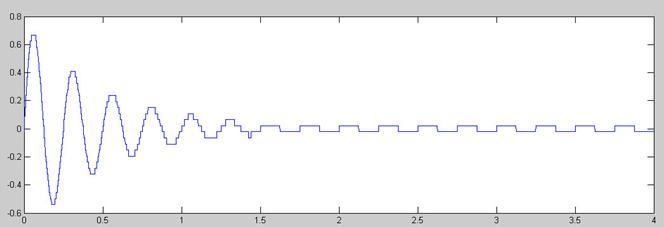
Señal Cuantificada Uniformemente
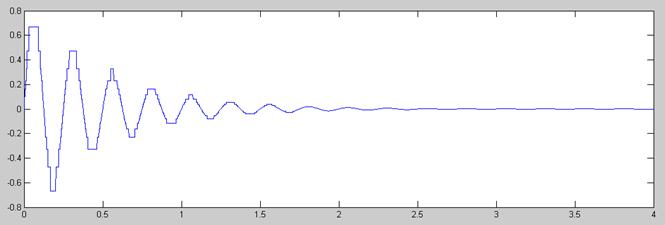
Señal Cuantificada no Uniformemente con Ley A
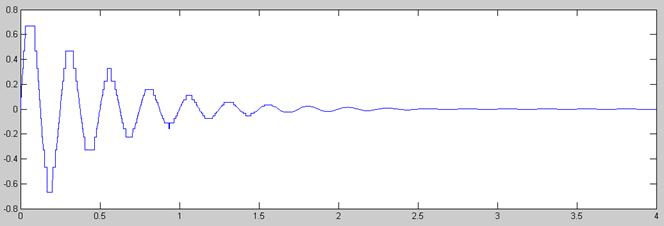
Señal Cuantificada no Uniformemente con Ley µ
Primeramente observamos que ls diferencias entre utilizar la ley A y la ley µ son mínimas, aunque a ligeramente a favor de la ley µ. Matemáticamente esta diferencia se representa en que la ley µ presenta una ganancia de compasión de 33.25db, mientras que para la ley A este valor es de 24.09 (para valores de µ=255 y A=87.6, respectivamente). Recordemos que la ganancia de compasión se define como la relación señal a ruido(de cuantificación) para señales de amplitud pequeña. Luego cuanta más ganancia de compasión, mejor.
En cuanto a la diferencia entre la cuantificación uniforme y no uniforme vemos que para amplitudes grandes, a partir de 0.2 Voltios, la cuantificación uniforme es claramente superior a la no uniforme, pues la señal es menos escalonada. Para valores amplitud superiores a 0.4 voltios la cuantificación no uniforme no es aceptable de ninguna manera, pues la diferencia entre el valor real y el cuantificado es enorme (recordemos que a mayor amplitud los escalones son más anchos). Sin embargo, para amplitudes inferiores a 0.2 Voltios la cosa cambia y se vé cómo la cuantificación no uniforme es claramente ganadora, pues los escalones son más estrechos y la señal aparece menos escalonada. En el intervalo final de la señal (tiempo>1.5 segundos) la amplitud es mínima y la ventaja de la cuantificación no uniforme aplastante, pues aparece como una señal casi exactamente igual a la original, sin apenas escalonamiento. Por el contrario, para estas amplitudes cercanas a cero la cuantificación uniforme no es aceptable de ninguna forma, pues está cuantificando con tan solo dos amplitudes distintas, por lo que la señal aparece rectangular.
Como conclusión, vemos que en este caso la cuantificación no uniforme es positiva pues aunque inicialmente perdemos algo de calidad cuando la amplitud es grande durante la mayor parte del tiempo esta señal tiene una amplitud pequeña, con lo cual queda mejor cuantificada que si se hubiera hecho de forma uniforme. Con lo cual, si la ampliar el número de niveles de cuantificación no es posible(pues haría aumentar el número de bits por muestra y eso no siempre es viable), la cuantificación no uniforme puede ser una alternativa.
En telefonía se utiliza mucho este tipo de cuantificación, pues la amplitud de la señal de voz es típicamente baja.
¿La cuantificación no uniforme es siempre la solución más eficiente? La respuesta es que si la señal se reparte de la
misma forma por todos los niveles de amplitud es mejor cuantificar de forma uniforme. Veámoslo con un ejemplo sencillo,
la señal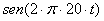 
, que como vemos se reparte equitativamente por todos los niveles.
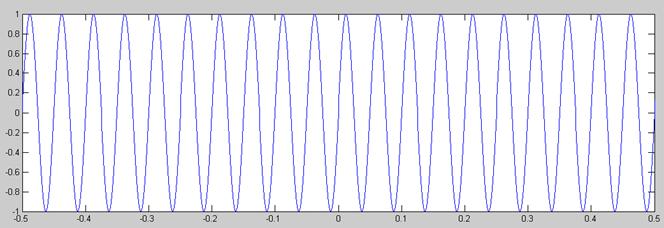
Señal original
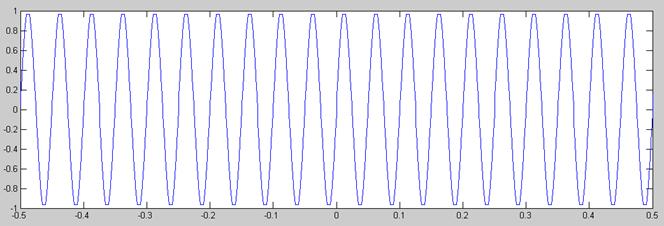
Señal Cuantificada Uniformemente
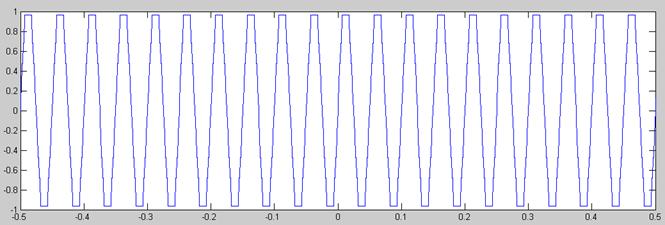
Señal Cuantificada no Uniformemente con Ley A
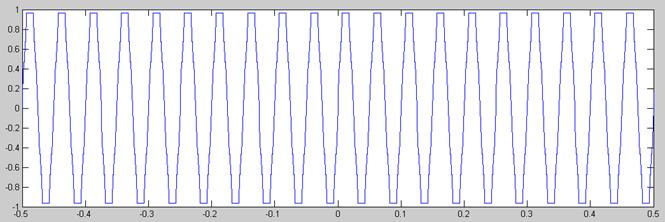
Señal Cuantificada no Uniformemente con Ley µ
En este caso las diferencias entre usar la ley A o la ley µ siguen sin ser significativas. En cambio si existen diferencias entre cuantificar uniformemente y no hacerlo, diferencias que posicionan la balanza a favor de la cuantificación uniforme, pues la señal aparece menos rectangular, especialmente para amplitudes superiores a 0.4 Voltios. Con la cuantificación no uniforme se asemeja más a una señal triangular periódica que a una sinusoide.
Hasta ahora hemos considerado el caso en el que el cuantificador estaba adaptado a la señal tanto en rango dinámico como en número de escalones.
Veamos primero qué ocurriría si cuantificamos la señal anterior con un cuantificador uniforme con el mismo rango dinámico pero menos niveles y, por lo tanto, anchura de escalón mayor. En este ejemplo se pasa de tener 32 niveles(ejemplo anterior) a tener solamente 4:
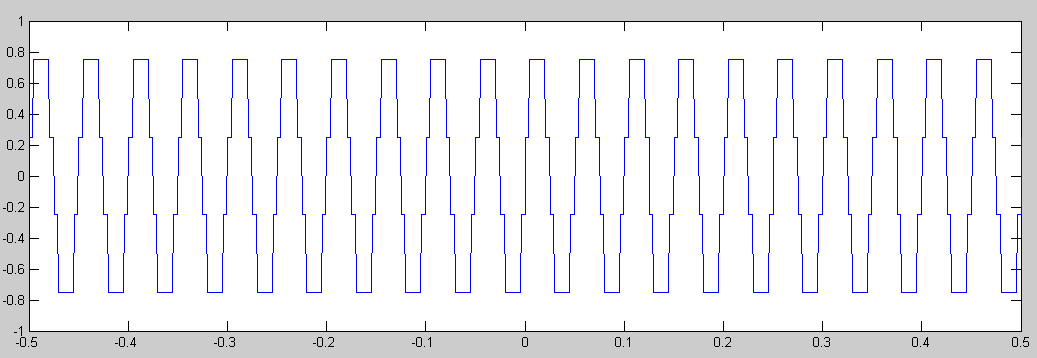
La pérdida de calidad es más que evidente y, de hecho, inaceptable. Sin embargo hemos pasado de tener que utilizar 5 bits ( a tener que utilizar solamente 2 bits ( . Con lo cual la señal, para la misma tasa de muestreo, ocupará 2.5 veces menos, lo cual puede ser interesante en algunos casos en que prime la velocidad de transmisión frente a la calidad.
Otra propiedad que hemos de ver a la hora de escoger el número de escalones del cuantificador es lo rápido que varía la señal: cuantos más rápido varíe más escalones serán necesarios para obtener la misma calidad. Por ejemplo, comparemos las señales rampa t y 3*t, ambas cuantificadas con 128 niveles(7 bits):
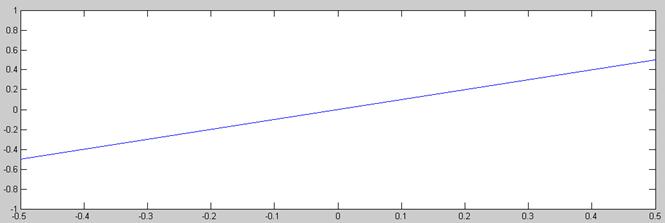
Señal Rampa t
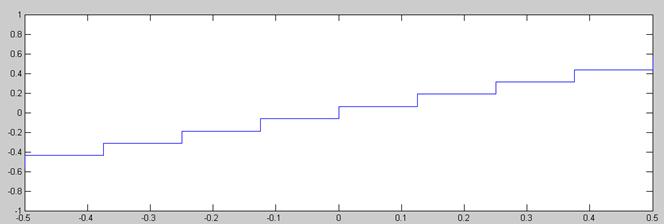
Señal Rampa t Cuantificada con 64 Niveles
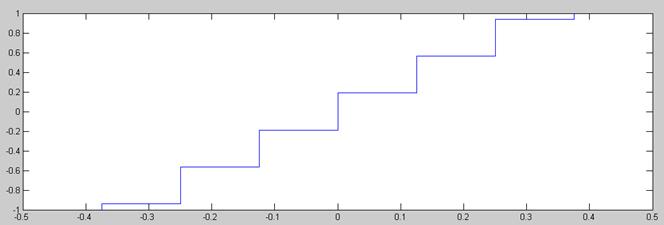
Señal Rampa 3*t Cuantificada con 64 Niveles
Otro parámetro a tener en cuanta al cuantificar una señal es el rango dinámico de la señal y del cuantificador. Lo ideal es que coincidan. Si el rango dinámico del cuantificador es mayor que el de la señal estaremos desperdiciando niveles de cuantificación y, si es menor, tendremos ruido de saturación (esto es, no podremos cuantificar los valores de amplitud más altos por salirse estos fuera del rango dinámico del cuantificador).
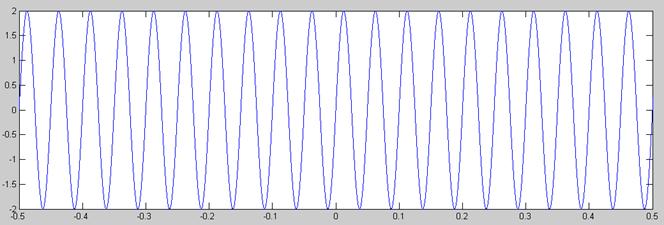
Para ello pongamos el ejemplo de las señales 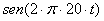y
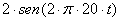usando el mismo cuantificador:
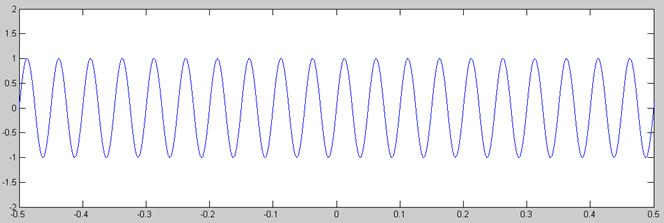
Señal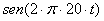
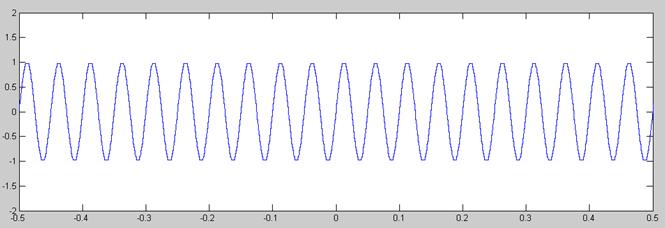
Señal 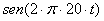cuantificada uniformemente
Señal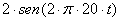
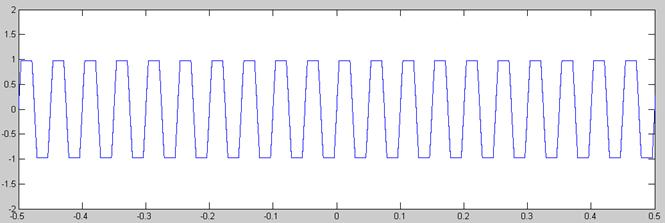
Señal 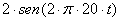cuantificada uniformemente
En la cuantificación de la segunda señal podemos ver 2 cosas: Primero, que aparece ruido de saturación, pues el margen dinámico del cuantificador se sitúa entre -1 y 1 Voltios mientras que el de la señal hace lo propío entre -2 y 2. Con lo cual, los valores superiores a 1Voltio (o inferiores a -1Voltio) no aparecen cuantificados. Y segundo, que la señal queda mucho peor cuantificada que en el caso del seno entre -1 y 1 Voltios, pues este segundo casa varía más rápido en amplitud (en el mismo tiempo que tarda la señal anterior en ir de -1 a 1 esta va de -2 a 2) y por lo tanto necesita más escalones para poder ser cuantificada adecuadamente.
Para terminar con la cuantificación, hablemos de la cuantificación diferencial. La cuantificación diferencial se utiliza sobre todo en señales de voz pues, debido a que en su espectro (de 300 a 3400Hz, típicamente) predominan las bajas frecuencias su tasa de variación es baja y, por lo tanto, la amplitud de 2 muestras consecutivas será bastante similar. Aprovechando esto nace la cuantificación diferencial en la que en lugar de cuantificar cada muestra de forma aislada se cuantifica y codifica la diferencia entre una muestra y la anterior. Como es lógico, el rango dinámico de la diferencia entre una muestra y la anterior es mucho menor que el de la señal total luego el número de niveles de cuantificación necesarios (y, por ende, de bits) será menor, disminuyendo así el bitrate y el tamaño del archivo.
Ya tenemos nuestra señal discreta tanto en tiempo como en amplitud, ahora sólo falta asignar un código a cada
muestra discreta. A cada posible valor cuantificado de amplitud se le asigna un código(una sucesión de 1’s y 0’s),
que tendrá un número determinado de bits, en función del número total de niveles a cuantificar que haya. En concreto,
si L es el número total de niveles de cuantificación y n es el número de bits por muestra, se tiene que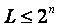 
.Aunque podemos tomar el L que deseemos (siempre que
Aunque podemos tomar el L que deseemos (siempre que 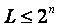) lo más eficiente es tomar el L máximo
(
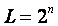)para así no desaprovechar ninguno de los niveles.A modo de ejemplo, si usamos
5 bits y usamos L=23 sólo estaremos usando 23 de los 32 posibles niveles, desaprovechando así 9 niveles. Una posible asignación de
códigos para cada nivel de cuantificación podría ser:
Donde se ha codificado asignando un número en binario mayor cuanto mayor es la amplitud (a la amplitud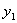 
le corresponde la codificación 001
y a la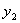 
la amplitud 100, por ejemplo. Al tener 6 niveles son necesarios 3 bits(pues con 2 podríamos diferenciar sólo 4 niveles distintos).
Hay que destacar que esta asignación es aleatoria, es decir, podemos asignar la codificación que deseemos a cada valor de amplitud (no tiene
por qué ser en binario creciente, como en este caso).
A modo de ejemplo se realiza la codificación de la señal |x|:
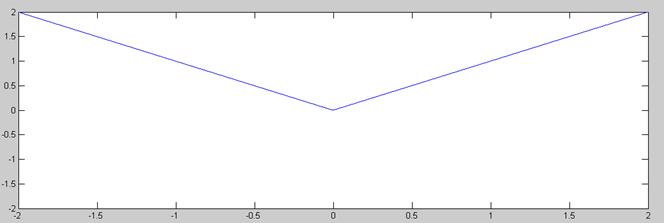
Señal |x| original
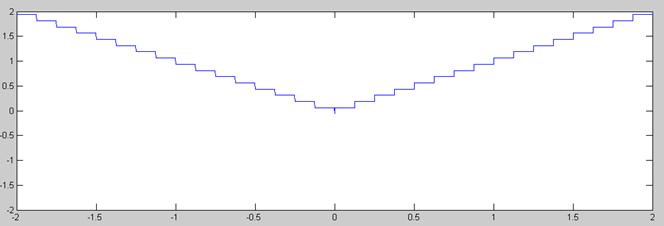
Señal |x| cuantificada con L=64 niveles y rango dinámico entre 0 y 2-(1/32)
Con la codificación tradicional codificamos cada muestra de forma independiente del resto asignándole su código correspondiente. Si la señal de interés tiene un alto rango dinámico y queremos un error de cuantificación bajo (es decir, que se puedan cuantificar diferencias de amplitud lo más pequeñas posibles) necesitaremos tener muchos niveles de cuantificación y, por lo tanto, tener muestras con más bits. Esto conlleva un mayor bitrate de transmisión y un mayor tamaño de almacenamiento de la señal.
Una posible solución a lo anterior sería cuantificar de forma diferencial,
teniendo en cuenta la muestra anterior. Para ello comparamos el valor de la señal
en el instante de muestreo actual (valor A) con el valor cuantificado en el instante
de muestreo anterior(valor B). Si el valor A es mayor que el valor B será por que la
señal está creciendo y, por lo tanto, el valor cuantificado actual será el valor anterior más un valor 
.
Si ocurre lo contrario, será el valor anterior menos . Esto es conocido como la modulación delta.
La modulación delta sustituye tanto a la cuantificación como a la codificación tradicional. Se utiliza
sobre la señal muestreada, es decir, no hay que cuantificar
previamente. El valor de se escogerá convenientemente. Graficamente:
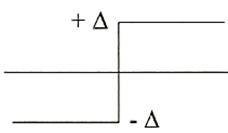
En este caso, la modulación delta se está haciendo con tan solo 2 niveles pero podría hacerse
con muchos más, con lo que el resultado final será más satisfactorio. Podría usarse esta modulación con
valores de 
, en función de cómo de grande sea la diferencia entre el valor
actual real y el cuantificado anterior. Pero esto incrementaría el número de bits por muestra (2 bits en ese caso).
Una señal cuantificada con la modulación delta de 2 niveles quedaría de la forma:
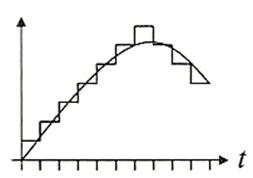
Sin más que echar un vistazo a la gráfica pueden obtenerse 2 conclusiones básicas:
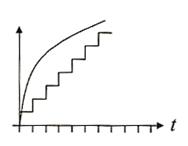
En concreto para no se de este caso ha de cumplirse que:
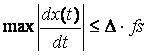
En resumen, con esta técnica pasamos de tener n bits por muestra a tener solamente 1.
Tener una altura de escalón de valor constante ( ) puede no ser lo más adecuado muchas veces. Con
el fin de subsanar este problema nació Adaptive Differential Pulse Code Modulation (ADPCM). éste sistema
trabaja al igual que la modulación delta, codificando la diferencia entre la muestra actual y la anterior
pero variando el valor del escalón de incremento/decremento (lo que antes denominabamos ) de forma dinámica en función
de la señal de entrada, para así poderse ajustar tanto a diferencias pequeñas como grandes.
Todo este extenso apartado puede resumirse en el siguiente esquema:
