Los Fractales y la Música Fractal 

Antes de nada, es necesario aclarar el concepto de fractal. Bien, un fractal es un objeto geométrico compuesto de elementos, también geométricos, de tamaño y orientación variable, pero de aspecto similar. Los objetos fractales tienen la particularidad de que al aumentar la escala de observación de dicho objeto, los elementos que aparecen vuelven a tener el mismo aspecto independientemente de cual sea la escala que utilicemos, y formando parte, como en un mosaico de los elementos mayores, es decir, estos elementos tienen una estructura geométrica recursiva, propiedad conocida con el nombre de autosemejanza.

       

                        

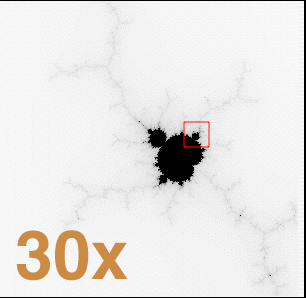
Arriba tenemos uno de los fractales más famosos, el Conjunto de Mandelbrot, del que publicaciones tan prestigiosas como la Scientific American han dicho de él que, hasta la fecha, es el objeto matemático más complicado creado por el hombre.

A la izquierda tenemos, el romanescu, un híbrido del brócoli y la coliflor,  ejemplo típico de estructura fractal natural.

A este tipo de formas geométricas que, entre otras propiedades, contienen una imagen de sí mismas en cada una de sus partes, se les llama fractales, y hace ya más de una década que inundaron el mundo científico con un conjunto de nuevas reglas para enfrentarse con el reto de conocer y describir la naturaleza. Su lenguaje se permeó a campos increíblemente diversos de las ciencias naturales y sociales, y ha hecho de las matemáticas un instrumento novedoso para las artes.

Las herramientas de la geometría fractal son, hoy día, elementos insustituibles en el trabajo de muchos físicos, químicos, biólogos, fisiólogos, economistas, etc., pues les han permitido reformular viejos problemas en términos novedosos, y tratar problemas complejos de forma muy simplificada. Las formas fractales, que durante mucho tiempo se consideraron meras "monstruosidades" geométricas e inaplicables divertimentos matemáticos, subyacen en fenómenos y estructuras tan variadas como la distribución de las estrellas del Universo, la ramificación alveolar en los pulmones, la frontera difusa de una nube, las fluctuaciones de precios en un mercado, y aún en la frecuencia de repetición de las palabras de este texto.

A la derecha tenemos otro ejemplo de estructura fractal: la hoja de un helecho vista a diferentes escalas presenta un aspecto semejante al de la vista en la escala original.

Hay fractales en los depósitos y agregados electroquímicos, y en la trayectoria de las partículas de polvo suspendidas en el aire. Fractales escondidos en la dinámica de crecimiento poblacional de colonias de bacterias, y detrás de todo flujo turbulento. Fractales en todas partes; fractales en una lista interminable de objetos reales que son testigos mudos de una interminable obsesión de la naturaleza.

Como entidades geométricas, los fractales tienen características peculiares. Imaginar curvas de longitud infinita que no se extienden en todo el espacio, o concebir un objeto con dimensión fraccional es el tipo de cosas que debemos estar dispuestos a enfrentar. Si la realidad es así, lo que debería asustarnos es lo que durante tanto tiempo concebimos como normal.

Los fractales han revolucionado la tecnología de la generación y reproducción de imágenes. Hoy día no sólo se les utiliza para almacenar o trasmitir señales visuales, sino también para simular paisajes. Hojas fractales para un árbol fractal en un bosque, un planeta, una galaxia digna de la más refinada película de ciencia ficción.

Los fractales parecen encontrarse en esa frontera difusa que existe en este mundo entre el caos y el orden; están ahí donde la imaginación apenas llega. De hecho, muchas veces se utiliza el término Geometría del Caos como sinónimo de Geometría fractal.

Música fractal

Beethoven, Bach y Mozart pasaron a la historia como grandes compositores. Pero, curiosamente, lo que reveló hace años el estudio de los fractales es que su música presenta ciertas propiedades fractales.

La coral situada al final de (Kunst der Fuge) (1749) de Johann Sebastian Bach es un ejemplo de pieza autosemejante. En ella los mismos motivos son repetidos una y otra vez con distintas variaciones dentro de una región mayor de la pieza. Así, por ejemplo, varias voces repiten al doble de velocidad la melodía de la voz principal (un motivo se repite por disminución a escalas menores).

Hay varios trabajos que analizan la manifestación de estructuras fractaliformes en composiciones clásicas: por ejemplo, en algunos se estudia la analogía entre la estructura del conjunto de Cantor y la primera Ecossaisen de Beethoven, así como entre el triángulo de Sierpinski y el tercer movimiento de la sonata para piano número 15, opus 28, también de Beethoven; en otros se analiza la autosemejanza de las fugas de Bach.

La música fractal intenta establecer los potenciales usos de la recursión, la iteración y las matemáticas complejas como una extensión de la composición musical. Así llegamos a que los fractales proveen una inesperada conexión entre las artes musicales y muchos procesos naturales, ya que mezclan cualidades deterministicas y estocásticas para producir naturalmente un agradable y no-estético balance entre predecibilidad y novedad. La estructura jerárquica del fractal autosemejante es análoga a la repetición y desarrollo de motivos musicales usados para crear unidad y coherencia en la música.

Actualmente algunos sintetizadores son usados para crear música techno con bases fractales. Cada vez son más los compositores que utilizan el caos o la geometría fractal como apoyo en sus composiciones. Una enorme cantidad de fractales puede ser fácilmente creado con un computador para ser usado como fuente inagotable de ideas musicales.

Texto extraído de un trabajo realizado para la asignatura Matemáticas en la Vida Cotidiana

durante el curso 2005/06,

por el autor de esta Web: Amir Al-Majdalawi Álvarez

(Para saber más acerca de los fractales, sus aplicaciones y su relación con la Teoría del Caos

puedes descargarte el documento original aquí: Trabajo Fractales (Amir 2006).pdf

 

---

Instrucciones simples producen gran diversidad en los cantos de los pájaros 

Físicos argentinos han conseguido imitar el complejo canto de los pájaros mediante un modelo matemático. El modelo simula la actividad de los circuitos neuronales encontrados en el cerebro de los pájaros, concretamente en el núcleo del cerebro que controla el canto y que es responsable de las señales que guían los movimientos vocales y respiratorios durante el canto. Haciendo que un modelo físico del órgano vocal de las aves obedeciera a las señales generadas electrónicamente por el modelo matemático, los investigadores han conseguido producir cantos sintéticos.

El experimento les ha permitido demostrar que determinadas arquitecturas simples en la zona del cerebro que controla el canto dan lugar a una gran diversidad de vocalizaciones. La investigación muestra cómo, también en el cerebro, comportamientos simples pueden dar lugar a resultados muy complejos, un fenómeno derivado de la dinámica no lineal e íntimamente ligado a la física del caos.

Compara un canto real (80 kb wav) con otro simulado (78 kb wav).

Investigadores:
Gabriel B Mindlin y Rodrigo Laje
Departamento de Física, FCEN, Universidad de Buenos Aires, Argentina.
http://focus.aps.org/story/v11/st1

Artículo de referencia:
Physical Review Letters (10/03/03) , 2002, Vol 8928, Iss 28, pp 8102

 

---

El nuevo sonido del violín (REVISTA MUY INTERESANTE) 

¿Puede la ciencia crear un violín que supere a los míticos Stradivarius?
 

Hacer Clic Aquí para acceder al artículo

 

---

La Música de las esferas 

Una antigua doctrina afirmaba que el modelo para la creación del universo estaba basado en el uso de las proporciones musicales. Según esta creencia, los cuerpos celestes producían sonidos que al combinarse formaban la llamada música de las esferas.

Hacer Clic Aquí para acceder al artículo

 

 Un satélite de la Nasa confirma la "música de las esferas", Diciembre de 2004

Hacer Clic Aquí para acceder al artículo

 

---

Hallazgo Músico-Cerebral